Quick Argument For Seximal

Intro

Quick explainer of what bases are: we use base ten, or decimal normally. This means the first digit of a number has a multiplier of one, the second digit of a number has a multiplier of 10, the third digit has a multiplier of 100, and so on. Ten to the power of the digit, starting from zero. This works the other way too. The digit before the first digit has a multiplier of one tenth. But what if we use a different value, like 6? Well then we have a ones, sixes, and thirty sixes (or nifs) column, and before the radix point (base neutral term for decimal point) we count by sixths. So 0.1 in seximal is one sixth.

Every base has that many digits. Base 10 has 10 digits, and base 6 has 6 digits. Those digits are usually 0 to b-1, and we won't be talking about anything unusual that breaks that convention. So seximal only uses the digits 0-5, since there's no need for 6 if 6 can be written as <10>.

NOTE: I will be using seximal for the rest of the article, unless I'm showing the way another base notates things! So just keep in mind that the second digit of a number is multiplied by six instead of ten. I'll also show the word name for the number so you don't get lost. The word and the number are not in conflict.

Example: "Stores often sell eggs in groups of 20 (twelve)". I didn't contradict myself, it's not twenty and twelve, it's twelve and twelve, just that I'm representing twelve as two sixes, rather than ten plus two. Because who cares about ten?

Size, Factors, Neighbors

Size

Some people prefer larger bases, but I think that in general, smaller bases work better, since they are more informationally efficient and the powers of the base don't get out of hand too fast. (That's why I like binary, but that's a topic for a previous time.) This is hard to argue over, as it is subjective.

People typically try to find a balance. The bigger a base is, the more digits you have to memorize and the more complicated math gets. Also, you lose the advantage of the powers of the base. But if it's too small, there's too many digits to remember per number rather than per system. I think that binary is a great base, but it is a bit tricky to use for everyday things, since it handles everything as well as decimal handles elevenths, while seximal handles the most important things really well. In other words, seximal is very conventional in comparison to binary, even if binary is "technically" superior.

Factors

14 (ten)'s factors are 2 and 5, so doing divisibility tests by 2 and 5 in decimal is easy, and the fractions for 1/2 and 1/5 are clean too. But 10 (six) has the factors 2 and 3, so divisibility tests by 2 and 3 are easy, and the fractions 1/2 and 1/3 are clean.

Neighbors

One less than ten (14) is nine (13), and nine is divisible by three (you can tell because I'm using seximal and it ends in a three!) so threes and nines in decimal aren't terrible to work with. But one less than six (10) is five (5), so seximal isn't terrible with fives, despite not having 5 as a factor. Doesn't it make sense to make 2 and 3 the easiest, and 5 the second easiest? As opposed to making 2 and 5 the easiest, and 3 the second easiest? Lastly is seven (11). Decimal is very bad with sevens, there's no divisibility tests* and the fraction is 10 (six) digits long and recurring. In seximal, the fraction is 0.05 with an infinite number of 05s afterward. Pretty simple!

*Okay, so, it turns out there kind of is. I don't know why no one else has mentioned this yet, but there's actually a bunch. Just google it. They're all a bit convoluted though, but I just thought I should mention that I was wrong about divisibility tests here.

Factors Continued

Powers of the Base & Composites

Seximal handles 2 and 3 perfectly, 5 pretty well, and 11 (seven) decently. Decimal handles 2 and 5 perfectly, 3 and 13 (nine) pretty well, and 15 (eleven) decently. But what about composites? Well we can use pairs of digits to act as the base squared. So 100 (six squared) is divisible by four. We could memorize nine different two digit combos, or, we could modify the digit sum test. The digit sum test actually works based on powers of the difference between the base and the number. Eg, multiply every digit by powers of 1 to test by 5, and multiply by powers of -1 to test by 11 (seven).

We can expand that to work with the base plus or minus anything. So to test by 4, or b-2, we multiply every digit by a power of two before adding them together. Like the number 124, 1*4 is 4, 2*2 is 4, 1*4 is 4, 4+4+4 is 20 (twelve), which we know is divisible by four, so the whole number is! We can do better, though. Because 4 is a factor of 10^2, we only have to do the last two digits.

In other words, double the six column and add it to the ones column. This is the divisibility test for 4 in seximal! (And in decimal, and every other even base not divisible by 4). This doesn't extend super far though, only to 12 (eight) as far as I know. for 12 (eight), you must check if the last 3 digits are a multiple of 12. To do this, multiply the nifs column by four, the sixes column by negative two, and add that all with the ones column. This is because eight is two more than six, it uses the powers of negative two. For 24 (sixteen) you have to check the last 4 digits, in which case dividing the last 4 digits by two and then checking divisibility by eight is much easier. Otherwise you'd have to use powers of negative ten...

Fractions

Seximal's fractions are very nice and simple. one half is 0.3 (three sixths), one third is 0.2 (two sixths), one fourth is 0.13 (one and a half sixths), one fifth is 0.1, one sixth is 0.1, and one seventh is 0.05. Decimal's fractions aren't too bad, but they're not as good as seximal's. One half is 0.5, one third is 0.3, one fourth is 0.25, one fifth is 0.2, one sixth is 0.16, and one seventh is... well I have to look it up now. If that's not proof enough I don't know what it is. Ah, it's 0.142857. Yikes!

Divisibility Tests

I mentioned divisibility tests earlier, but I didn't go into much detail. I'll continue. In seximal, if a number ends in a multiple of two it's even, if it ends in a multiple of three the whole number is a multiple of three. To check by five, add up all the digits and check if that's a multiple of five. To check by seven, add up all the pairs of digits, so for example 3,3403, 3 + 34 + 03 is 44, which is a multiple of seven! This works because one less than nif is divisible by seven. Alternatively, you can do an alternating sum thing. Invert the sign of every other digit, and add them together. Is it a multiple of seven? So with the example from earlier, 3,3403 becomes 3 + -3 + 4 + -0 + 3, or 11. Which one is more complicated depends on which base you're using and personal preference.

Dozenal

Lots of people like base 20 (twelve). I think it's bad for two main reasons: it's bad with fives and sevens, and it's large. One fifth in dozenal is 0.2497, and one seventh is 0.186X35 (I'm using X for the ten symbol and E for the eleven symbol). Also, single digit quarters are very gimmicky. You don't need repeats in the prime factorization. A base should try to be smaller and then let the powers of the base repeat those primes for them.

Flaws

No base is without compromise. Seximal sucks with eleven and dozen one, and probably most primes after that. it just has no way to handle them. No divisibility test, and the fractions suck. One eleventh is 0.0313452421 (14 digits). One dozen first is 0.024340531215 (20 digits). These are terrible, but, they are fairly large primes, and the reciprocals of primes in most bases are either a 1 digit long repeating section, or an even number of digits. When it's an even number, that means that the second half plus the first half is all b-1's. Also, there's only 10 possible states for each digit instead of the normal decimal 14. So you have to remember a 5 and 10 long string of digits in base 10 (six), which, you know, isn't great but it's a major improvement on what it was before.

And actually, edit from the future here: seximal has a divisibility test for every prime, because every non trivial prime is 10n plus or minus one. It works like this: remember what multiple of 10 (six) it's one off from, and call that k. Then take the last digit of the number you want to test, multiply it by k, and add it to the rest of the number. (The rest of the number just means floor(n/10) by the way) Except if it's one more than a multiple of 10, then you subtract it instead of adding it. Keep doing this recursively until you get to a multiple of the prime. Pretty cool huh?

That was hard to follow, here's an example. Let's test 34 (twenty two). Eleven is one less than 20, so we'll multiply the last digit by 2. 4 * 2 = 12, and 12 + 3 = 15. That one was easy. Let's try testing by dozen one. Let's try 5102. Start by multiplying the last digit by 2, so now we have 510 - 4, which is 502. Then it's the same thing, 2 * 2 = 4, 50 - 4 = 42. 2 again, so 4 - 4 = 0. 0 is indeed a multiple of dozen one, so it's divisible! I think this settles the binary vs seximal debate. Binary's main thing is that it handles all primes. Sure, this doesn't tell you anything about the fractions, but I really don't care about fractions past 1/11, even sevenths are pretty meh. At that point I'll just use a calculator. Something that is better about binary is that with it being so small, the 14 digits recurring for 1/15 are very easy to memorize. Because there's only 2^14 possible states, and the second half is the bit flip of the first half as discussed previously. So there's really only an info space of 2^5, which is why one eleventh (along with every other binary fraction) is so easy to memorize compared to every other base. But, I care about terminating thirds way more than memorizing elevenths so it's pointless.

Dozenal advocates will say "yeah, you have to give up fives, but that's just the price for threes and fours" which is super silly because seximal does threes, fours, AND fives, whilst being half the size! (Though, in my experience, most dozenalists see being small as a downside not an advantage.)

Conclusion

That concludes my argument for seximal, I think. I may have forgot something. In conclusion, seximal is pretty cool and conventional enough to be actually used sometimes. If this interests you, check out jan misali's seximal website! It inspired this webpage and is the only reason I know about seximal. (Well, the video he made that links to his website, but still) It's like this webpage but higher quality and longer. Lastly, I designed my own seximal symbol set. Here are the digits in order, 0-5: , , 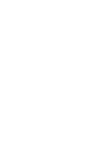, , 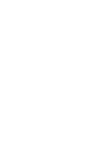, . They're not particulalry good or anything, but I think they're pretty and I like using them.

I made a dice set with them! (And a 3D printer)