Introduction
I like numbering systems. Do I like seximal or binary more? I don't know! Seximal feels more "flavorful" in a way, and it's definitely more conventional than binary. Binary is extremely weird and different, and while being the most informationally efficient mathematically, it doesn't feel that way when using it. Binary is like the purest form of math and numbers, without resorting to regular polygons or dots, but seximal feels like the more human, more artsy- while still being very functional- number system. Powers of two just feel robotic and mathematical, while the powers of six feel pretty. I don't know, I'm talking completely about subjective vibes here. Anyway, here's my binary systemplex. (A systemplex is a word I made up just now that means a system of systems)
The point of this webpage is to cover everything necessary for adopting binary as a system for writing numbers, instead of decimal. I plan to update it over time. It is not meant to be me arguing for the case of binary, and this webpage is written with the assumption that you already think binary is the best base, or don't know what "best base" even means.
Note: I will be using binary (or one of its powers) to represent every number. For the sake of clarity and compactness, I'll usually write it in its word form, but oftentimes I'll write it as a number. Depends on the context/how I'm feeling.
This webpage (of course) is inspired by this video about how binary is the best base, and jan Misali.
Notes For Normies (You can safely skip if you're a nerd)
I tend to... forget that not everyone is super used to thinking about other bases. I understand not getting them intuitively (that's hard and takes hours of practice! I only barely get seximal and binary in that regard) but I do forget that not everyone understands them logically, either. Like one time I was showing someone jan Misali's video about seximal and they were confused by the part about dozenal when he said "counting by twelves". They said that he wasn't "counting by twelves" because it went <10>, <20>, <30>, instead of <12>, <24>, <36> even though it was established SECONDS ago that we were counting in dozenal, where the second column is the twelves column! Anyway this wasn't meant to be a section to make fun of people, but rather to make this webpage more accessible-
Getting back on track. Here's how bases work logically: every symbol is associated with a value, and each digit location is associated with a multiplier. The first digit is a multiplier of 1, the second digit is a multiplier of the base (so like two or six or ten), and the third digit is a multiplier of the base squared. The fourth digit is the base cubed, and so on. Then past the radix point, so zero point something or <0.X>, is a multiplier of 1 over the base. One sixth in seximal or one tenth in decimal. Then the second digit is one over the square of the base, so one one hundredth in decimal or one nifth in seximal. Or one fourth in binary. That's the basic run down of how bases work, I hope the explainer image can help solidify things a little. It shows the number <135.2> in seximal, spoken as "one nif thirsy five point two". As the fraction is two sixths, it is equal to one third, or <0.333> in decimal. The integer part of the number is 36DEC plus 3*6=18DEC plus 5DEC. Which equals 59DEC.
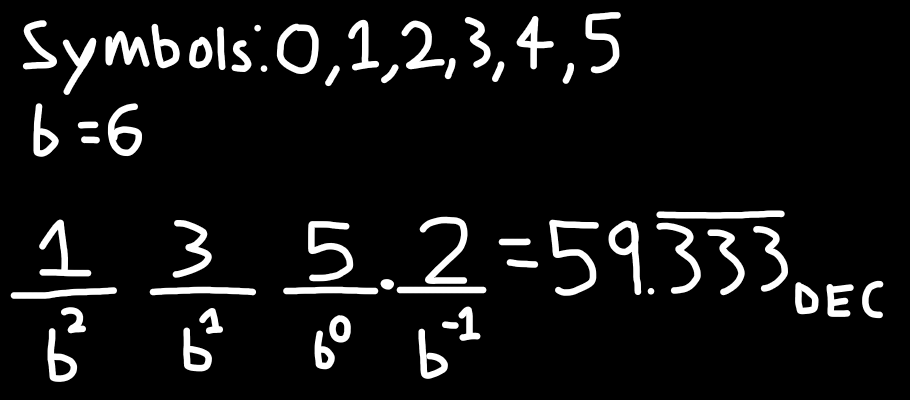
ALSO after finishing making that image I realized it's a bit confusing- the horizontal dashes are meant to be digit places. The number on top is the symbol that represents a value, and the number below is the multiplier decided by positional notation. They totally look like fractions. Oops.
What you need to know to understand this webpage: assume every number is written in binary unless stated otherwise. Decimal numbers are denoted like thisDEC. So, using binary means that the second column is not for tens but for twos, and the third column is not for hundreds but for fours, and the fourth column is for eights, and so on. Every next column is worth twice the value of the last. So when you see the number <10>, it means the value two, not ten. And don't feel dumb or inadequate if you read it as ten- I often read the numbers in decimal before correcting myself. If I was able to write this whole thing whilst doing that, then you can still read and understand it. It doesn't mean you're "not smart enough" or anything. People often say they're not smart enough to understand when I show them something, not realizing that I struggle with it/have struggled with it in the past.

Same thing here. Again these are not fractions (except for the fractions) but digit places. Value on top, multiplier on the bottom. It's like the opposite of a fraction.
Second thing: words' values never change. When I say "ten" some people (in my experience) think it means <10> and its value is context dependent on what base we're using. This webpage doesn't do that. "Ten" always refers to two times five.
Third thing: The angle brackets <> mean "notation", or "writing", rather than raw value. So like, if I were to suddenly be talking about how seximal writes the number 100 (remember! This is four not one hundred), I would say it represents it as <4>. That's what the brackets mean. Very important to know what they mean, it's kind of abstract but fairly intuitive I hope. Also by the way this is a very standard and common thing, I did not make it up. Don't get angry at me if you think this is arbitrary!
So yeah, as long as you understand that 10 is two, 100 is four, 1000 is eight, 1,0000 is sixteen, and 0.1 is
half, you should be good! Assuming you have perfect memory and logical reasoning and read this webpage in order,
you should be able to understand it. One more thing: The number ten comes up a lot. I sometimes write it as "ten",
or 1010, but sometimes I write it as ʔ because that's one of the few tessimal* digits I can write in
unicode and I'll be DAMNED if I don't use it.
*One other thing is that tess is 16DEC, so tessimal means what most people would call hexadecimal. I don't like the name hexadecimal for fairly obvious reasons, I mean it means 110 + 1010. Very base 1010 centric.
I hope this was enough for you to understand my webpage! I'm always sad when I fail to teach someone something, so I thought I'd throw in this segment to help people adjust to my craziness. This webpage will make more sense if you've seen the binary video listed at the top. But it's over an hour long so I don't expect anyone to watch it, and it's not strictly necessary. Have fun.
Writing System
Compression
Binary small. How do we fix this? Well, compression. Binary works best with other bases as friends, to support it. It works best with power of two bases, obviously. In the original video, they used a short bar for zero and a tall bar for one. I think this has some problems, mainly that they're not distinct. So let's put a dot above the one for a further distinction. Also, if you don't want to group them into twos/fours with an underscore, we can combine them into a single symbol. Here's my symbol set:

This system is designed to be flexible, but if that's too open ended for you, there is a standard: Convert the number to tessimal (it's not difficult, just look at every four bits and then use the look up table) then cut off the leading zeroes on the most significant digit by using a bit and or pair. Example: 1,0000 is converted to "i∩", and 10,0000 is converted to "Y∩" (not entirely accurate, the Y like character should be a lot thinner). Alternatively, you can use octal or quaternary and do the same thing. It's really not recommended to just fully use quat or tess, for spatial and informational efficiency reasons. But it's your life man, I can't control you.
I'm really happy with my tessimal symbols, here's how they work. You've got a symbol for 0 (∩), 100 (L), 1000 (ʔ), and 1100. Then you put a strike through it for +10, and a dot towards the top for +1. Every odd number has a dot, and every number divisible by four lacks a marking. This should make it easier to convert from and to pure binary, which will hopefully give back some of the simplicity that's lost.

Wait but, isn't this not binary anymore? Well yeah, actually, it's not. It's called mixed radix. But it's just as efficient as binary informationally, and can be converted back to pure binary very easily, so I think it's fine. Information theory is a little unintuitive, but basically, since bits are the smallest unit of information, we use them to measure things. Take decimal. One decimal digit costs 100 bits. So the number "two" takes 100 bits to write in decimal, but only two in binary. That's why it's the most efficient base. It works for large numbers too, the number 10,000DEC in decimal costs 1,0100 bits because it's 101 digits long and every decimal digit costs 100 bits. But that value translated to binary is 10,0111,0001,0000, which is six bits less!
Shifting our focus back to the compression image, notice how I grouped the bits into fours. Since one tessimal digit costs 100 bits, we can replace any group of 100 bits in the middle of a binary number safely, without changing its informational cost. Likewise, we can swap out any 10 bits with a quaternary digit. That's exactly what my system does. These are called quads and pairs respectively. Someone could argue that my system is still binary, I'm just displaying groups of bits weird. I really don't know the "rules" of this. You can view it either way, I don't care, this system only exists to make things easier to write without interfering with the informational efficiency of binary, and I achieved that goal I think.
Remember: When writing binary on a computer, you can use 1s and 0s for simplicity. You should group them into fours with commas, just like decimal does in threes. Similarly, tessimal should be grouped into twos, but it only really needs this grouping after 4 or so digits. It doesn't matter as much as the grouping in binary does, as long stretches of zeroes and ones are hard to parse at a glance. And in quaternary you should group them into fours.
Math
It's recommended not to mix them like a filthy animal, as that makes math difficult. In order to do math, the numbers must be using the same system.
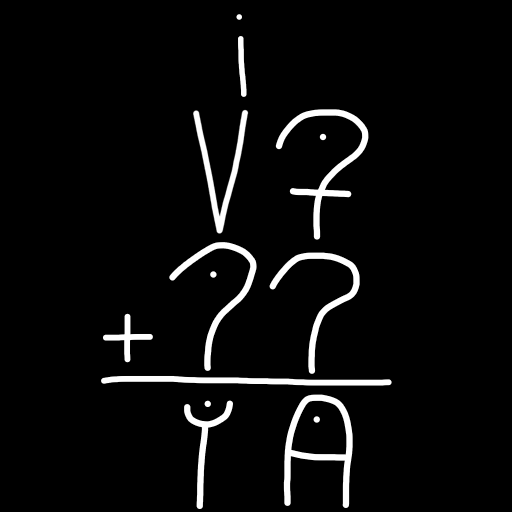
If this math looks complicated, that's okay, new symbols are hard. But remember, binary addition is really easy, so if you don't think you can add single digit eleven and eight in your head, just remember that the glottal stop is eight and the dot is one and the dash is two. So this is eight plus eight plus two plus one. These symbols are designed in a way to make math easier. First you add the base symbols together, which is like adding two quaternary numbers together, and then you add the dots and dashes, which is like another pair of quaternary numbers. But if you can't handle that, you can rewrite the equation using pairs or bits.
You could also just say "quads are too much, I'm only gonna use pairs" and that works too! You can also just use the aforementioned pure binary grouped into quad clusters from the binary video.
Fractionals
What about the not whole numbers? Well mark the radix point with a period, and mark when the digits start repeating with an apostrophe. I recommend using pure binary for the fractional part, and to put a comma every four digits, except going right instead of left of course.
Verbal System
Quads
| 0, ∩ | Zero | |
| 1 | One | |
| 10 | Two | |
| 11 | Three | |
| 100, L | Four | |
| 101 | Five | |
| 110 | Six | |
| 111 | Seven | |
| 1000, ʔ | Eight | |
| 1001 | Nine | |
| 1010 | Ten | |
| 1011 | Eleven | |
1100,  |
Twelve | |
| 1101 | Prim | 1101 is prime, so, prim. |
| 1110 | Dusep | 1110 is two times seven, so dusep. |
| 1111 | Thirpen | 1111 is three times five, so thirpen. |
You're not going crazy, I did recently rename some numbers. Currently I only renamed tripen to thirpen, but I'm thinking about renaming some others.
Next there's names for the powers of tess. The "ek" suffix means 10n. Dozek is 10 to the power of 1100, or a dozen. The "el" suffix means 1010n.
| 1,00001 | Tess | Tesseracts have this many vertices. Feels like four squared. |
| 1,000010 | Octek | I'd call it byte but bytes are units of information. |
| 1,000011 | Dozek | |
| 1,0000100 | Tessek | |
| 1,0000101 | Vigek | "Vige" means 1,0100. Base 1,0100 is called vigesimal. |
| 1,0000110 | Tetrasek | Tetra is four, sex is six, four time six is tess and eight. |
| 1,0000111 | Quadroseptek | Quadro is four, sept is seven, four times seven is tess twelve. |
| 1,00001000 | Pentel | |
| 1,00001001 | Nifek | Nif means 10,0100, or two tess four. |
| 1,00001010 | Quadragesek | It means four times ten ek. |
Now we put it all together by reading the number in each column followed by its place, skipping zeroes. Take the number "
 ". It's
pronounced "One tessek five dozek nine octek and twelve". The number is pronounced "five thousand five hundred and
thirty two" in decimal. My system is one syllable longer, with eleven syllables.
". It's
pronounced "One tessek five dozek nine octek and twelve". The number is pronounced "five thousand five hundred and
thirty two" in decimal. My system is one syllable longer, with eleven syllables.
Pairs
Pairs work just like decimal, except in groups of four, and with different names, of course. In decimal, you take
each group of three digits and read them as if they were on their own, and then append the proxy base
ʔ11 digit's location. Example: the number <9,560,241> is read as "nine million, five
hundred sixty thousand, two hundred and forty one". The first group of three has no name, the second group of
three has the "thousand" suffix, and the third group of three has the "million" suffix. So let's do the same
thing!
Of course, the numbers zero through four will have the same names. But then, just like decimal, let's make the numbers <0-13> have unique names before going to a system! For clarity, we'll just name these zero-seven, and have eight or <20> be called "octy". So 12PAIR is called "six", but 23PAIR will be called "octy three". And for <30> let's call it "dozy" because three times four is dozen.
Also, I'm really struggling to figure out when to use angle brackets and when to use subscript "PAIR". So I apologize for the inconsistencies, I swear there's some grain of coherence in there.
For <100>, we'll call it "tess" for obvious reasons. We won't make names for multiples of <100> as decimal doesn't either. With this system <2132> is pronounced as "two octred one tess and dozy two". Or "two octred tess and dozy two", either works, but I prefer the former. In quads this is
 and is pronounced as "nine tess dusep".
and is pronounced as "nine tess dusep".
By the way, I'm using 0-3 for simplicity and typability's sake, but don't forget that the real symbols are
 .
.
| Powers of Four | x1 | x10 | x11 |
| 1001 | four | eight/octy | dozy |
| 10010 | tess | ||
| 10011 | octred | ||
| 100100 | octek | ||
| 1001000 | tessek | ||
| 1001100 | tetrasek | ||
| 1001,0000 | pentel |
The system is finished! Let's try it out with a big number of pairs. We'll use <23,1000,2033,0013> for the example. It is pronounced "octy three tetrasek, one octred tessek, two octred and dozy three octek, and seven." Here's a decimal equivalent number (not equivalent in value, but equivalent in types of digits used and number of digits. Very important distinction!) <98,100,602,004> is pronounced "ninety eight billion, one hundred million, six hundred and two thousand, and four." Well, I think we did it! Those sound very similar! Goal accomplished.
Bits
In the original video, the system for speaking binary numbers presented was very complicated, but in a strange way, simple and elegant. I will take it as a starting point and improve upon it, or at least try to.
The way it works is you split your number at the largest meta power of two, so for this example let's use the number 10,1101. We split that into 10 and 1101, or two and prim. We remember the name for that meta power of two (in this case tess) and keep it in the middle.

This is a little confusing, but it'll make sense in the end. Next, we just repeat that recursively.

Notice how we split the 10 into the two side and the one side, and only wrote the two side because it has a one in it.

Now we look at prim, or 1101. We split it after the second place, keeping in mind that anything on the left side of the split is multiplied by four. We write "four" for this purpose. Next we split 11, and write "two one" since both digits are one. We don't have to split the 01 part on the right side at all, since the two's place is zero. The ones place is one, so we write "one". With me so far? I hope so because that's it, we're done! Let's do another example since this is a bit tricky to follow.
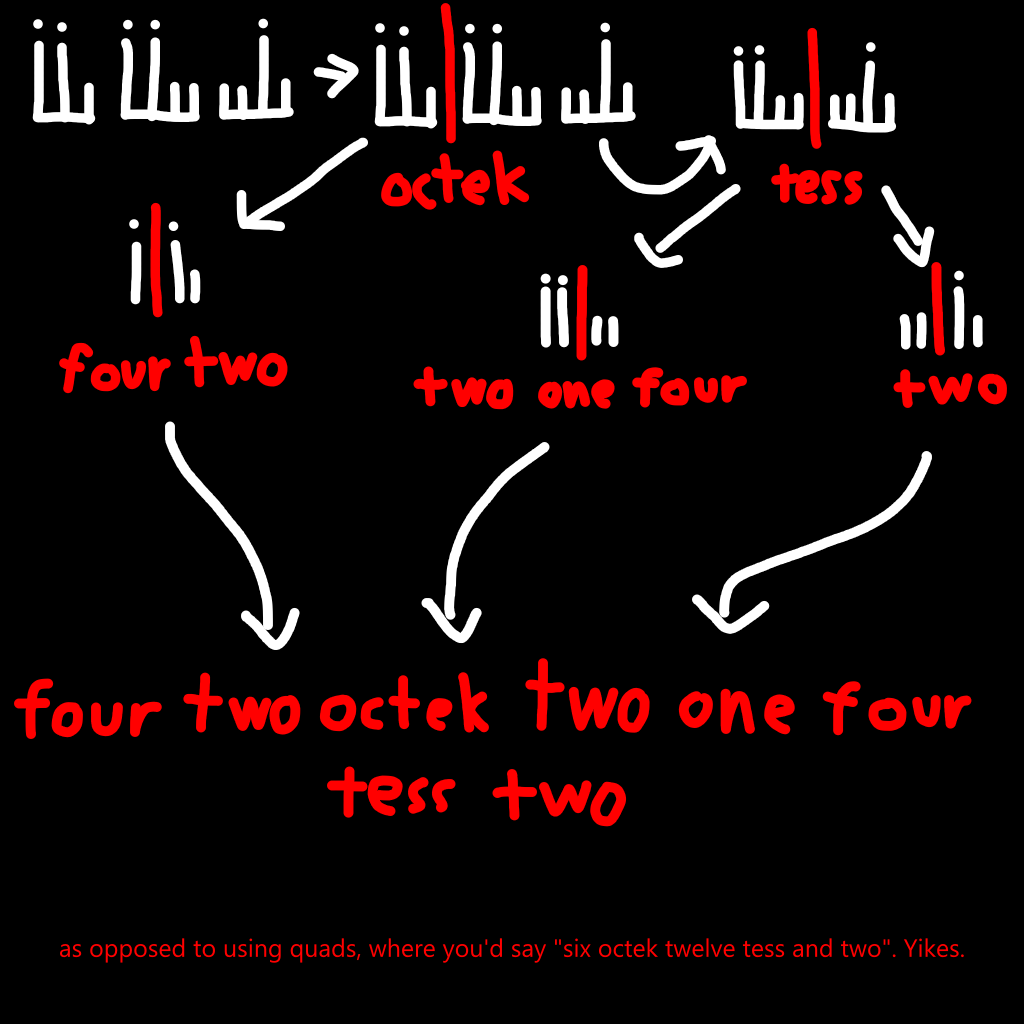
As you can guess from the addendum, I don't really reccomend using this. It's long, it's complicated, and it's somewhat unclear... at first glance. But if you use it for a little while, it's surprisingly intuitive. It's still very long though, so let's fix that! But first, I should explain how to go from text to number.
Start at the largest power of two (in this case octek), and split each side recursively. So "four two octek" and "two one four tess two". With "four two", the numbers descend in value, so we add them to get six. With "six octek", the numbers increase in value, so we multiply to get six octek. With the second part, let's start with the first pair. "two one" is descending so we add them to get three. "Three four" is ascending, so we multiply them to get twelve. Technically, we're supposed to split this block to be "two one four tess" and "two", but it's pretty easy to do mentally, and I don't want to make this needlessly long.
The next pair is "twelve tess". It goes up, so we multiply. We could go "(twelve tess) two", but that's incorrect, as the meta powers of two are supposed to be separated, as I mentioned previously. In this case the result will be the same, but not always. If instead of two it was two four, which is supposed to be eight, this wouldn't work and would just add six. Now that we have our three numbers (six octek, twelve tess, and two), we just add them together to get our final number, 110,1100,0010. That's correct!
Before we get into improving this system, I want to try something. Right now it feels very quads/tessimal like, so let's go past twelve bits long. Running the math, 11,1111,0100,1001,0001,0000,1011 is... "two one octek two one four two one tess four tessek two four one tess one octek two four two one"! Wow that is a mouthful. It took me a solid 5 minutes to translate. I'm not sure if it's because I'm unpracticed, but still this system... isn't great. I recommend using quads, or at least pairs. One thing I do like about this method is that it feels very binary (no abstraction) and it's very fun to count in.
one, two, two one, four, four one, four two, four two one, two four, two four one, two four two, two four two one, three four, three four one, three four two, three four two one, tess.
Alright it's time to improve this. The only thing the original video did was replace the very common "two one" with "three". We'll do that as well, but I want to go further. But it's tricky to go further, like what if we make "two four" "eight"? Then twelve could be written "three four", or it could be written "eight four". Also I'm not sure if it will interefere with the whole meta powers of two thing. I don't think it does. But it is annoying how it makes multiple ways to do different things. Like how "three eight three" means three times eight plus three, or tess eleven, but it could also be written "tess eight three", and that's not just ignoring the new system, like how "two one" being "three" is perfectly fine, you just can't say "two one" anymore.
I think I have a solution. It came from thinking about three. Because it's not a meta power of two, you can't use it as the second part of a multiplied ascending pair. Eg, nine is always "two four one", and it's never "three three". So you can't do "three eight" to talk about tess eight. You have to call it "tess eight". Hey, that's a number where quads and bits call it the same thing, neat! Actually, pairs call it the same thing too! I'm not sure if this is a good or bad thing. I think it's a good thing, since it doesn't matter which system you're using. It would be bad if "two tess" meant something different in one of the systems, because then you wouldn't know what number is being described.
That fixes one problem but that still leaves the three four/eight four problem. I suppose I just pick one. Hmm. Okay, after thinking for a while, whenever there's a choice when you're converting, favor addition. In decimal, <150> is "one hundred and fifty" not "tree fiddy", and I think that makes sense. It feels the most natural doing that when counting.
one, two, three, four, four one, four two, four three, eight, eight one, eight two, eight three, eight four, eight four one, eight four two, eight four three, tess.
Okay I think that worked! I hope I didn't miss anything and accidentally make this system unusable with ambiguities. If there's multiple ways to write one number, that's unfavorable, but not the end of the world, but if there's two numbers that share a written form, that is the end of the world. Literally everyone on Earth would die and then the core would start nuclear fusion and become a very small star. I was a little worried at the end, because I wanted to type "two eight" but then remembered you're not allowed to do that. I think this works. Let's try it on big numbers, starting with the one from earlier!
110,1100,0010 is pronounced "four two octek, eight four tess, two". I also figured we could use commas to make things easier, though that does slightly conflict with counting. Oh well.
11,1111,0100,1001,0001,0000,1011 is "three octek eight four three tess four tessek, eight one tess one octek, eight three"! Yeah, this is still really hard to understand. It doesn't have the biggest thing first, which is strange. Or I guess, all things do that. "Two hundred" technically has a small thing first. With this double spacing system though, the beginning small part before the big part just gets larger and larger.
The first example is a syllable decrease of 1, and the second example is a syllable decrease of 1000! Honestly the first one was a really unlucky example. Anyway, I'm done yapping, so here's the chart.
| 1010n | Name |
| 10 | Two |
| 100 | Four |
| 1,0000 | Tess |
| 10ʔ | Octek |
| 10i∩ | Tessek |
| 10Y∩ | Pentel |
| 10L∩ | Hexel |
| 10ʔ∩ | Septel |
| 10i∩∩ | Octoplex |
| 10Y∩∩ | Enneael |
Some things aren't meta powers of two but are included anyway, as discussed previously.
| n | Name |
| 1 | One |
| 11 | Three |
| 1000 | Eight |
Ordinals
Ordinals are just pronounced like normal numbers except the last digit is different. It's just a carbon copy of English, lol.
| 1 | First |
| 10 | Second |
| 11 | Third |
| 100, L | Fourth |
| 101 | Fifth |
| 110 | Sixth |
| 111 | Seventh |
| 1000, ʔ | Eighth |
| 1001 | Nineth |
| 1010 | Tenth |
| 1011 | Eleventh |
1100, 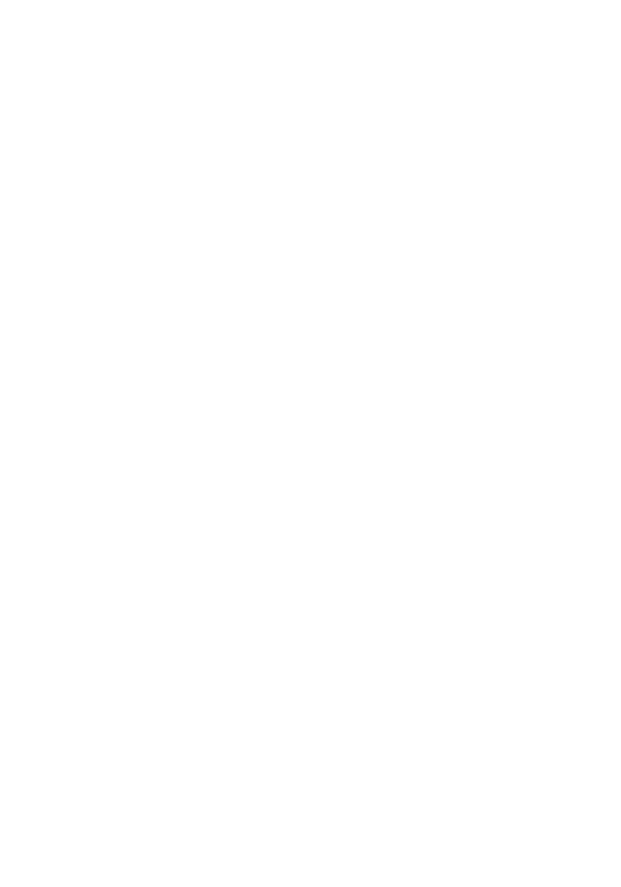 |
Twelfth |
| 1101 | Primth |
| 1110 | Dusepth |
| 1111 | Thirpenth |
Fractionals
How do we deal with the part after the radix point? Well it's pretty simple. It works basically identically to how it does left of the radix point, but with reciprocals of natural numbers instead of powers of two. Like how you wouldn't call "0.333" "zero point three three three" when you could instead say "one third". You can also use the standard method but flipped horizontally, ignoring all fractions but powers of 1,0000, but I recommend using the other fractions and using pure bits. Like, you could say 0.1 as eight tesseths, or you could just say one half.
For terminating ratios, you have two options. The first is to start from the radix point and go to the right, moving down this chart by one row per digit. Every time there's a one, say the name that corresponds to that digit, if there's a zero, skip it. This is a complicated way of saying "split it into its component fractions". Here's an example: 0.0010,11 would be read as "one eighth, one half tesseth and one stacketh". This works but is clunky.
The second method is to use the number of digits as an index for this chart (one digit after the radix, first row, three digits after the radix, third row) and then just read it as a normal number followed by the fraction. Eg: 0.011 is "three eighths". This seems better but runs into problems with numbers like 0.1000,1. Method one works better with that number as it says "a half and a half tesseth" rather than "tess and one half tesseths". Maybe that's okay. It's subjective.
My actual favorite method is a mix of the first two, where you use method one but combine groups of consecutive ones and then use method two on those. That's a little confusing- here's an example: 0.1011,0111 Method 1: "a half, eighth, tesseth, stacketh, hecteth, and octekth", Method 10: "eleven tess and seven octekths" Hybrid: "a half, three tesseths, and seven octekths". While it's slightly less compact than method 10, it's certainly more understandable. You get the most important info first and immediately know it's a bit more than a half, and exactly how much more than a half it is.
| Multiples of: | Name: |
| 0.1 | Half |
| 0.01 | Quarter/Fourth |
| 0.001 | Eighth |
| 0.0001 | Tesseth |
| 0.0000,1 | Half Tesseth |
| 0.0000,01 | Stacketh |
| 0.0000,001 | Hecteth |
| 0.0000,0001 | Octekth |
If you run into the limits of this system, use the standard digit grouping method and then read them out sequentially just like decimal does.
What about ratios that don't terminate? Which in binary, is literally any fraction that is not a multiple of a reciprocal of a power of two, yikes. Well, you can try to identify its fraction and then speak that with its multiple, but I only went to sevenths because after that it's hard to recognize multiples. So I don't actually have an elegant system for this... you just read the bits in order and pronounce the repeating mark as "rep".
| Multiples of: | Name: |
| 0.'01 | Third |
| 0.'0011 | Fifth |
| 0.0'01 | Sixth |
| 0.'001 | Seventh |
This may seem pretty bad- and it is, binary's biggest weakness is its non-integers, but I'd argue it's okay as bits are very easy to remember. I mean, binary is definitely better at representing fifths then dozenal, despite having the same number of digits before repeating in both bases. That's because for those 100 digits, there's tess possibilites in binary but in dozenal there's five dozek and an octek possibilities! So memorizing it is- in theory- much harder in dozenal than binary. 1/1011 and onward though, it is pretty difficult to remember, some of those strings are very long. But still, it's only one bit per digit. Whenever a larger base stumbles a fraction, it could be any one of the b digits, but when binary stumbles a fraction, it can only be one of two digits.
Measuring System
To make a measuring system you need two things: affixes for the powers of 10, and definitions of units. The actual definition of the unit doesn't matter, as it's one of itself so it will always feel convenient, whilst being completely arbitrary.
Unit of Length: The Ferret
The ferret is defined as 10,1010.0011,0110,0100,0101,101 centimeters, or exactly twice the hydrogen wavelength. It's also roughly the length of a ferret. It's also 42.212cm in decimal, for calculators.
Unit of Mass: The Fennec
Defined as the mass of a proton times 10(10110 + 1,1001), or 1.0000,1000,1111,0101,11 kilograms. A fennec fox weighs between 0.1011 and 1.1001,1 kg.
Units of Time
Units of time are very complicated, as they should be defined based on the rotational period of the Earth, and not
physicsy stuff. Previously, I had a really arbitrary unit here but I've now replaced it with something sensible.
This will also describe how time keeping as a whole works. For the sake of simplicity, one day will be defined as

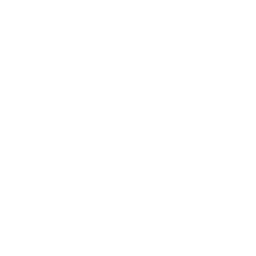


 seconds. (Just over one and a quarter tessek).
seconds. (Just over one and a quarter tessek).
The day will be divided into six equal parts called macros. Six is a very nice number, as it's an SHCN. (Superior highly composite number). A macro is exactly four hours long. Then, there are waits, which are octekths of a macro. These are the stand in for minutes, and are 11,1000.01 seconds long. Finally to get our version of seconds, we divide by four tess to get 0.1110,0001 seconds. These are called ticks. Great now we have a binary hour, binary minute, and binary second!
Lastly, let's shift everything back one macro. So hour 0 to hour 100 will be macro 5 instead of macro 0, and 100 to 1000 AM will be macro 1, and so on. This sounds confusing, and is a layer of complexity, but I think it's worth it. We think of today and tomorrow being relative to when we sleep, and our system should reflect this. When you stay up to 11 AM, you don't think "wow it's really early in the morning", you think "wow it's really late in the night". So that's why 0 to 100 AM is the fifth macro instead of the first.
Decimal definitions for your calculator needs:
| Macro | 14400 Seconds |
| Wait | 56.25 Seconds |
| Tick | 0.87890625 Seconds |
Because they're based on powers of two, they all terminate. Very handy.
Powers of 10
| 10-(10110 + 1,0000) | Insignifi- | |
| 10-(10110) | Teeny- | |
| ... | ||
| 10-1,0000 | Itsy- | |
| ... | ||
| 10-1000 | Byter- | |
| 10-111 | ||
| 10-110 | Stacker- | |
| 10-101 | ||
| 10-100 | Tesser- | Sounds too similar to Tessa, might change later. |
| 10-11 | Eighter- | I like this idea of -er meaning 1/x. |
| 10-10 | Quarter- | |
| 10-1 | Semi/Hemi- | |
| 100 | None, one | |
| 101 | Duo- | |
| 1010 | Quadro/Quatro- | |
| 1011 | Octo- | |
| 10100 | Tessa- | A tesseract has i∩ vertices. |
| 10101 | ||
| 10110 | Stacki- | Stack because of minecraft. |
| 10111 | Hecto- | This is stolen straight from decimal. They aren't using it so it's okay. |
| 101000 | Byto- | |
| ... | ||
| 101,0000 | Grande- | Very big. A meta power of 10. |
| ... | ||
| 1010110 | Colossa- | |
| 1010110 + 1,0000 | Ultra- |
You may notice that some spots are missing, or sucky. I will try to fill them when I get good names for them, but in the meantime you can combine them to go bigger. You can technically write any power of two suffix by doing that, but in practice "colossacolossacolossaferret" sounds really bad. So the suffix for squaring is "bi-", and cubing is "tri-". After that you're screwed I guess. Also, I couldn't figure out a way for 101000 and 10-1000 to get good octek related prefixes, so I used byte.
Some Examples
Alright now that we've defined our measuring system, we can use it for stuff!
The speed of light is

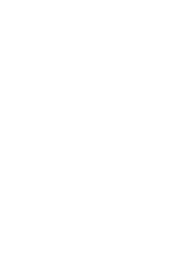





 and a half ferrets/tick. This number is pronounced as "two quadroseptek, five tetrasek, three vigek, four tessek,
nine dozek, prim octek, three tess and thirpen."
and a half ferrets/tick. This number is pronounced as "two quadroseptek, five tetrasek, three vigek, four tessek,
nine dozek, prim octek, three tess and thirpen."
The weight of the Earth is
 colossafennecs. This number is pronounced "four tessek, twelve dozek, five octek, prim tess
and eleven colossafennecs."
colossafennecs. This number is pronounced "four tessek, twelve dozek, five octek, prim tess
and eleven colossafennecs."
The distance between the earth and the sun is one astronomical unit. It's also
 grandeferrets. Spoken as "five vigek
two tessek eight dozek three octek ten tess and dusep and an eighth and three stackeths."
grandeferrets. Spoken as "five vigek
two tessek eight dozek three octek ten tess and dusep and an eighth and three stackeths."
Arithmetic And Divisibility Tests
This section will take a lot from the video this webpage is inspired by. As binary is the simplest base, its math is very simple too. Addition is an XOR and an AND. What does that mean? Well if you want to add two one digit binary numbers, there's two outputs: the sum and the carry. If we treat 1 as true and 0 as false, the sum is simpy "A XOR B", which means "A or B, but not both", and the carry is "A AND B" which is super simple! This is how computers add numbers under the hood. But then what about adding three numbers, like A, B, and the Carry? Well it's trivial for humans so I won't bother explaining the logic behind it.
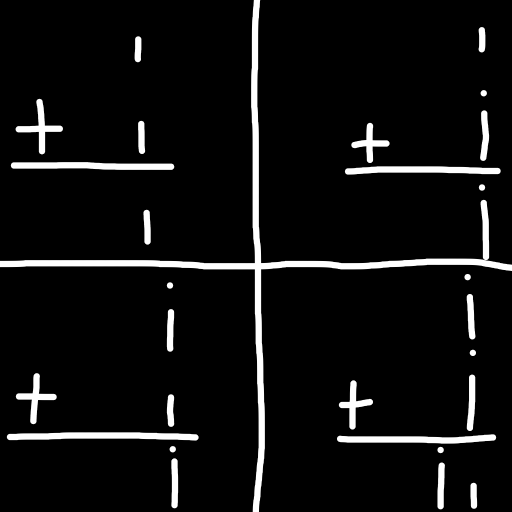
For multiplication, it's even simpler. You just put a copy of the first number at every 1 of the second number, and then add them. Be careful of digit misalignment.
Counting
Counting is really important. This method for finger counting I'm about to explain is actually so good that I use
it. Usually when people make stuff advocating for one base or system, they understand that standardization is much
more important than how practical a system is. Doing math in decimal is a pain in the ass, but if you show someone
<30> and they think you mean three tens instead of three sixes, that could be really bad. Obviously, I'm not
advocating that we switch to binary or seximal as the mathematical benefits would be far outweighed by the price
of having to change EVERYTHING to use the new system, and then having to deal with confusion about stuff made
before [year we decide to change] being written in base ʔ (ten). Anyway, if you need to count items
and don't need to show the number to anyone else, this is what I do: it's just the standard binary counting
method. If you're nerdy enough to be reading this webpage you already know what I'm about to explain.
So basically, every finger is its own binary digit. Curled means zero, and extended means one. I use my thumb as the least significant bit on both hands (but you'll usually only need one hand). Even if you don't think in binary (I certainly don't. I think in seximal more often than I think in binary) binary finger counting is still worth it! (In my personal opinion) You just have to memorize the powers of two up to five, and then you can add them in your head. (You may also need to memorize how they add together). Here's a diagram:
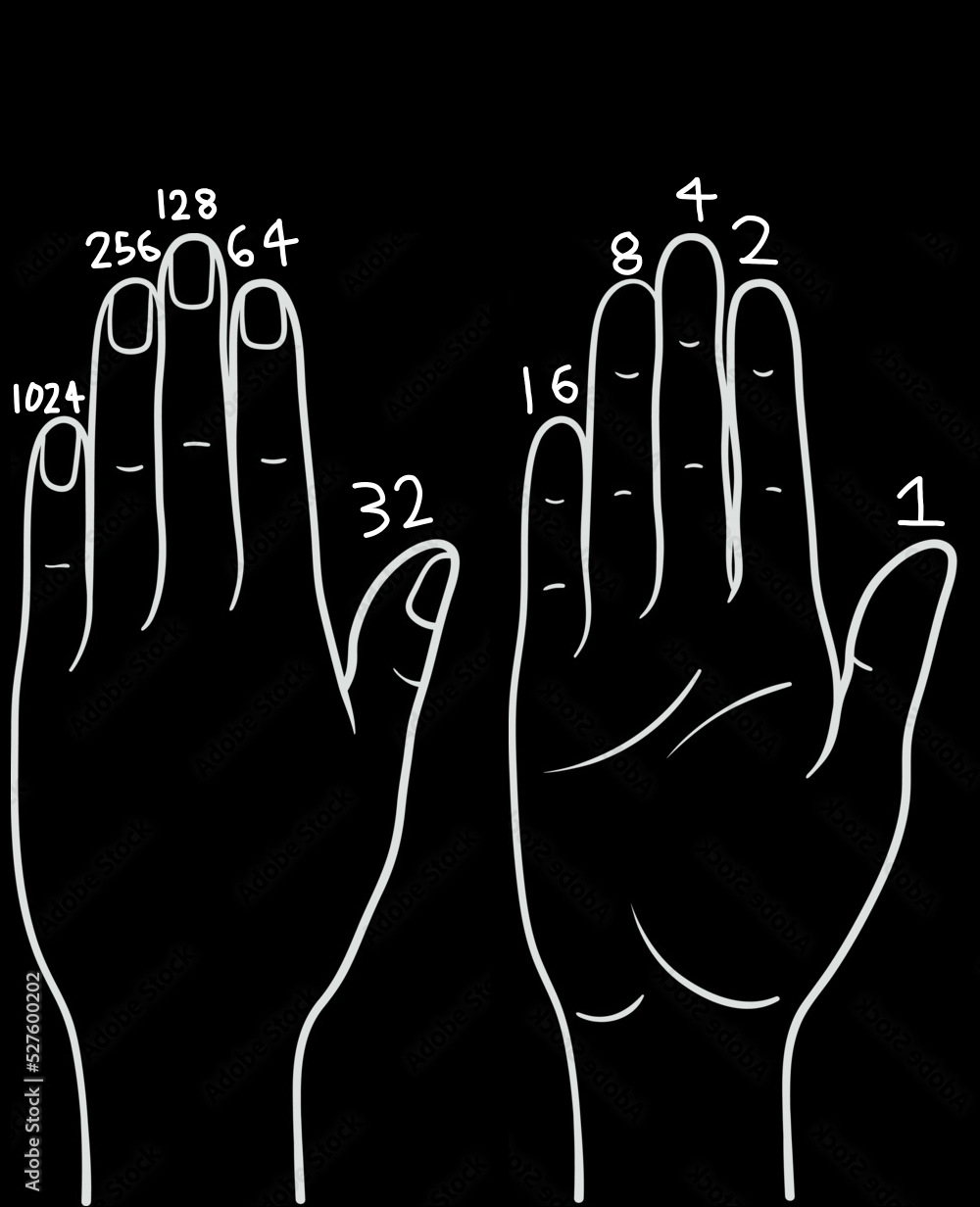
My way of finger counting is actually a bit unusual (according to a quick google search of "binary finger counting") but this is what comes naturally to me and it's the easiest for me. Also that google search had a result that was backwards, and would only work for people looking at your hands, which is just stupid. If you think my method is a bit illogical and convoluted, just realize that both thumbs are the least significant bit of their hand. I can't move my pinky fast enough to be the ones counter, and the thumb, pointer, and middle are the easiest to extend individually.
What I like about this method is that it's very flexible (as long as you don't need to show the numbers to other people), so if you can't move two fingers independently, just fuse them together! And if you like to count from your pinky, do that! Also I've written the numbers in decimal because of what I said earlier about how this system is still great in decimal (or really any base), and that's the base humans seem to like, so I thought it would be most useful to write it in decimal. One last thing I'll say is that this makes a pretty good fidget. Sometimes I binary finger count if I'm bored. I'm enchanted by the satisfying rhythm of it!
Magic Sequence
The magic sequence is a really interesting sequence that every integer has. Basically, if you have a number N, to find its magic sequence you start with 1 and at every step double it. If it's greater than N, subtract N. Keep going until it becomes a number it's already been (because that means it will loop) now you have the magic sequence! This is a little confusing, mostly because of how arbitrary it sounds. So here's another written example, for the number seven. The magic sequence for seven is one, two, four, and now it's not eight because that's over seven. Eight minus seven is one so that's the next term in the sequence. It will loop one two four forever. Now here's eleven's magic sequence:

"Okay, but what's the point?" Well it can do two things: checking divisibility, and generating fractions. These two operations are actually kind of the same thing.
For this example, we'll be testing if 111,1001 is divisible by 1011. The number we're checking we'll call A, and the number we're checking if A is divisible by we'll call B. So, spread out the digits of A and write the magic sequence of B backwards (so increasing powers of two go to further and further terms of the magic sequence). Next, add up all the terms of the magic sequence that are under a 1. In this case, we got the result of "10,0001". We repeat this process again: The first term of eleven's magic sequence is one (just like every magic sequence), and the sixth term is ten. Ten plus one is eleven, and eleven is divisible by eleven so we just proved that 121DEC is divisible by eleven in binary! Which is very cool. Binary has a doable divisibility test for EVERY integer. It does get a bit cumbersome with numbers with a lot of ones, though.

Lastly, we can use a similar method for figuring out the binary expansion of ANY fraction. Even primes! Take the magic sequence of the number you want to find the reciprocal of. Mark the inbetween points of the sequence with a 0 when it increases, and a 1 when it decreases. Make sure to include the last term that completes the loop (in this case 1). If it doesn't end with a 1 that means it's composite, and that means it can have a non recurring part, like one sixth. One sixth has a magic sequence of 1, 10, 100, 10, 100, and so on. It loops two and four forever. So using the fraction method, that gives us 0.001010101... which is completely correct! One sixth is 0.0'01 in binary. And actually, you only need to do half of any prime sequence. The other half of the expansion is just the first half with its bits inverted. No really, look at it! Every binary expansion has an even number of digits in the recurring section. Even simple fractions like one sixth follow this rule. The recurring part is "01" the second half being the inverse of the first.
How does any of this work? I don't know, I got this from the binary video and it didn't explain it.
It's a good idea to memorize these to save yourself the trouble of making them every time.
Numbers
Here's a big ol' list of numbers and how they're written, starting at 1 and going up to one octred. I stayed up until 3 AM writing the code that made this list! It was fun, but also very very difficult. Here's a MUCH bigger list that goes to dozek (101100).
| Binary | Quaternary | Tessimal | Mixed | Quads | Pairs | Bits |
 |
 |
 |
 |
One | One | One |
 |
 |
 |
 |
Two | Two | Two |
 |
 |
 |
 |
Three | Three | Three |
 |
  |
 |
  |
Four | Four | Four |
 |
  |
 |
  |
Five | Five | Four One |
 |
  |
 |
  |
Six | Six | Four Two |
 |
  |
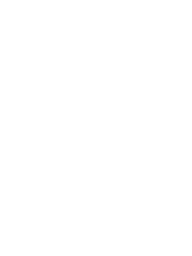 |
  |
Seven | Seven | Four Three |
 |
  |
 |
 |
Eight | Octy | Eight |
 |
  |
 |
 |
Nine | Octy One | Eight One |
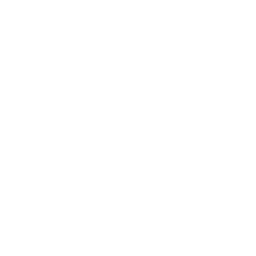 |
  |
 |
 |
Ten | Octy Two | Eight Two |
 |
  |
 |
 |
Eleven | Octy Three | Eight Three |
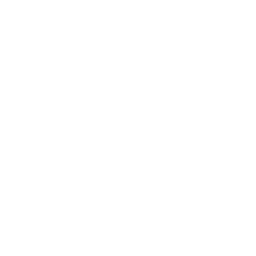 |
  |
 |
 |
Twelve | Dozy | Eight Four |
 |
  |
 |
 |
Prim | Dozy One | Eight Four One |
 |
  |
 |
 |
Dusep | Dozy Two | Eight Four Two |
 |
  |
 |
 |
Thirpen | Dozy Three | Eight Four Three |
  |
   |
  |
  |
Tess | One Tess | Tess |
  |
   |
  |
  |
Tess And One | One Tess And One | Tess One |
 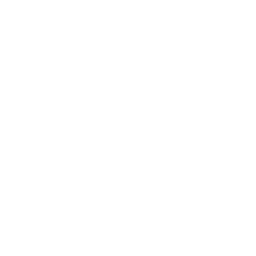 |
   |
  |
  |
Tess And Two | One Tess And Two | Tess Two |
  |
   |
  |
  |
Tess And Three | One Tess And Three | Tess Three |
  |
   |
  |
  |
Tess And Four | One Tess And Four | Tess Four |
  |
   |
  |
  |
Tess And Five | One Tess And Five | Tess Four One |
  |
   |
  |
  |
Tess And Six | One Tess And Six | Tess Four Two |
  |
   |
  |
  |
Tess And Seven | One Tess And Seven | Tess Four Three |
  |
   |
  |
  |
Tess And Eight | One Tess And Octy | Tess Eight |
  |
   |
  |
  |
Tess And Nine | One Tess And Octy One | Tess Eight One |
  |
   |
  |
  |
Tess And Ten | One Tess And Octy Two | Tess Eight Two |
  |
   |
  |
  |
Tess And Eleven | One Tess And Octy Three | Tess Eight Three |
  |
   |
  |
  |
Tess And Twelve | One Tess And Dozy | Tess Eight Four |
  |
   |
  |
  |
Tess And Prim | One Tess And Dozy One | Tess Eight Four One |
  |
   |
  |
  |
Tess And Dusep | One Tess And Dozy Two | Tess Eight Four Two |
  |
   |
  |
  |
Tess And Thirpen | One Tess And Dozy Three | Tess Eight Four Three |
  |
   |
  |
  |
Two Tess | Two Tess | Two Tess |
  |
   |
  |
  |
Two Tess And One | Two Tess And One | Two Tess One |
  |
   |
  |
  |
Two Tess And Two | Two Tess And Two | Two Tess Two |
  |
   |
  |
  |
Two Tess And Three | Two Tess And Three | Two Tess Three |
  |
   |
  |
  |
Two Tess And Four | Two Tess And Four | Two Tess Four |
  |
   |
 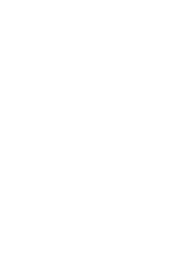 |
 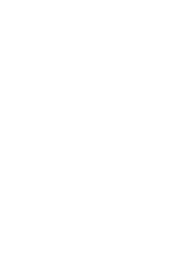 |
Two Tess And Five | Two Tess And Five | Two Tess Four One |
  |
   |
 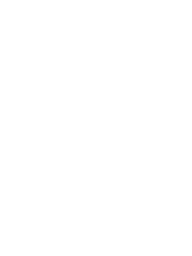 |
 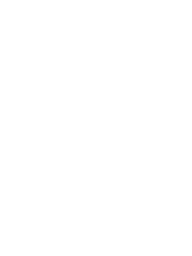 |
Two Tess And Six | Two Tess And Six | Two Tess Four Two |
  |
   |
  |
  |
Two Tess And Seven | Two Tess And Seven | Two Tess Four Three |
  |
   |
  |
  |
Two Tess And Eight | Two Tess And Octy | Two Tess Eight |
  |
   |
  |
  |
Two Tess And Nine | Two Tess And Octy One | Two Tess Eight One |
  |
   |
  |
  |
Two Tess And Ten | Two Tess And Octy Two | Two Tess Eight Two |
  |
   |
  |
  |
Two Tess And Eleven | Two Tess And Octy Three | Two Tess Eight Three |
  |
   |
  |
  |
Two Tess And Twelve | Two Tess And Dozy | Two Tess Eight Four |
  |
   |
  |
  |
Two Tess And Prim | Two Tess And Dozy One | Two Tess Eight Four One |
  |
   |
  |
  |
Two Tess And Dusep | Two Tess And Dozy Two | Two Tess Eight Four Two |
  |
   |
  |
  |
Two Tess And Thirpen | Two Tess And Dozy Three | Two Tess Eight Four Three |
  |
   |
  |
  |
Three Tess | Three Tess | Three Tess |
  |
   |
  |
  |
Three Tess And One | Three Tess And One | Three Tess One |
  |
   |
  |
  |
Three Tess And Two | Three Tess And Two | Three Tess Two |
  |
   |
  |
  |
Three Tess And Three | Three Tess And Three | Three Tess Three |
  |
   |
  |
  |
Three Tess And Four | Three Tess And Four | Three Tess Four |
  |
   |
  |
  |
Three Tess And Five | Three Tess And Five | Three Tess Four One |
  |
   |
  |
  |
Three Tess And Six | Three Tess And Six | Three Tess Four Two |
  |
   |
  |
  |
Three Tess And Seven | Three Tess And Seven | Three Tess Four Three |
  |
   |
  |
  |
Three Tess And Eight | Three Tess And Octy | Three Tess Eight |
  |
   |
  |
  |
Three Tess And Nine | Three Tess And Octy One | Three Tess Eight One |
  |
   |
  |
  |
Three Tess And Ten | Three Tess And Octy Two | Three Tess Eight Two |
  |
   |
  |
  |
Three Tess And Eleven | Three Tess And Octy Three | Three Tess Eight Three |
  |
   |
  |
  |
Three Tess And Twelve | Three Tess And Dozy | Three Tess Eight Four |
  |
   |
  |
  |
Three Tess And Prim | Three Tess And Dozy One | Three Tess Eight Four One |
  |
   |
  |
  |
Three Tess And Dusep | Three Tess And Dozy Two | Three Tess Eight Four Two |
  |
   |
  |
  |
Three Tess And Thirpen | Three Tess And Dozy Three | Three Tess Eight Four Three |
  |
    |
  |
   |
Four Tess | One Octred | Four Tess |
Money
Money is said to be responsible for the rotation of the Earth. I think angular momentum and the history of the solar system is to blame, but I'm no economist, or astrophysicist. This part is kind of silly because the bills I designed are only half serious and kind of stupid looking. They're only mock-ups of what the money could look like. Also, I'm from the United States so I will be designing a system for USD. United States currency famously depicts presidents, but as I'm a math nerd and this is a nerdy money system I'm designing, so I decided to use famous mathematicians instead.
Picking Values
A 1 dollar bill seems like a good place to start. I thought about adding a 10 dollar bill, but then realized it's kind of worthless. You can just use two one dollar bills. That's why people don't use two dollar bills, even though they exist. Having a four dollar bill seems like a good idea, as tess is a bit too large to include just a half-of-the-base bill. (This is a webpage about binary and we are using binary, but since binary is very small it's helpful to pretend we're using tessimal when you want to pull out nice round numbers.) I'm using the American system for inspiration here- there's the one, two, five, and ten dollar bills. So we should have a one dollar bill, a half tess (eight) dollar bill, and a tess dollar bill. (No two because as estabilished it's not necessary) But the problem becomes obvious: eight dollars is kind of a lot compared to one dollar. Think about the worst case, where something costs seven dollars. You hand them an eight dollar bill and they give you back seven one dollar bills. No. That's madness. We need a 100 dollar bill.




In the US's system, the next bills are identical but multiplied by ten. They have a twenty dollar bill, fifty dollar bill, and one hundred dollar bill. Twenty dollar bills are actually handy, so I'll include the equivelant here. (Two tess). Then I decided to just have every power of two between tess and octek. So we've got a two tess, four tess, eight tess, and octek dollar bill.




Design
Obviously these are a little ugly, and that's okay, they're just to be a rough sort of prototype. In each corner is the value of the bill written differently. Top left is bits, top right is pairs, bottom left is quads, and bottom right is the hybrid/standard system.
Most of the mathematicians were chosen at random, but some of them have a bit of thought. Here's all of them:
On the tess dollar bill, I put Gottfried Wilhelm Leibniz. This is because he invented binary, and tess is a very binary related number. It's 101010.
On the four tess bill I put Matt Parker because he's the youngest mathematicians listed here (in terms of birth date, as opposed to the age when the photo was taken, their age at death, etc), and he's done a few videos about Minecraft, so he probably at least kind of likes it. And Minecraft gave a very popular name to the number four tess, stack. If this sounds like a stretch, it is, but most of the other bills don't have any rhyme or reason to which mathematician is put on them.
I put Alan Turing on the octek bill. This is because he did a lot with computer science and so the number associated with bytes seems fitting.
Coinage
What about values less than a dollar? Well I only have one coin for that, the quarter. I'll explain why- in 1793, there was a coin called the half penny. As you'd expect, it's value was one two hundredth of a dollar. But in 1857, it was retired for being worth too little. But here's the interesting thing- when you adjust for inflation, it's worth 18DEC cents today! Which means that we should only have quarters as coins. So that's why I only have a quarter. Also the image for the quarter is really bad, krita doesn't handle curving text well and I was lazy at this point as I had just done 1000 bills beforehand.

There's a zero and a one across the two sides, this is to solidify the connection between flipping a coin and a random bit. Also makes heads/tails a little clearer, as it's just zero and one. And that's about all I have for money.
Published 1/14/2025, or 1/1110/111,1110,1001