My Favorite Shapes!

In this page I try to sort shapes I like into an ordered list, whilst trying to remain sort of objective and not putting a bunch of shapes that look pretty but aren't interesting mathematically. Maybe I'll do a "shapes I like" page later. Also, wow, sorting favorites is really hard. Several times through writing this page I shuffled the order of things around, or found loops, where I liked A more than B, B more than C, and C more than A. Basically what I'm trying to say is that this order is very fuzzy and should not be taken seriously.
Every image on this page is by me.
List
10th - 6-6 Duoprism
"Hey, doesn't this break your rules about aesthetic judgements? This is just some random ass duoprism."
Well, yes, but I have my reasons! This is an n-n duoprism, meaning its noble and has 3 flag orbits. There are an infinite number of these, but the 6-6 duoprism is sort of special. It's the most complex duoprism to tile E4 on its own! It makes perfect sense that this can tile, but I still think it's really cool for some reason. Also, because it's isotopic, convex, and has central inversion symmetry, it makes a fair die! Okay yeah this one is mostly subjective just "I like it".
9th - Tesseract

"Same with this one! This is some random n-cube! There's like, over a dozen n-cubes, why this one?"
Because!!! It's related to the 24-cell. This is the only n-cube with a rank greater than 2 to have a demicubic vertex figure, and it has a diagonal of 2. Both of these facts help to construct the 24-cell. The diagonal thing fuels the cubic pyramid explanation, and the demicubic vertex figure fuels the 16-cell demicubic explanation. I'll go in depth more on the latter in the 16-cell's section, but as for the cubic pyramid explanation:
As I'm sure you know, attaching 8 CRF cubic pyramids to a tesseract creates a 24-cell. This is because the CRF cubic pyramid has a height of 0.5. This is because its square pyramid facets want to be √2 units tall, half an octahedron, and when they do this, the cube spacing them out 1 unit turns the whole pyramid into a sort of "two right triangles" scenario, where you have half a square, cut along the diagonal. In this case, the longest edge is 1, and the height is 0.5. I hope that made sense.
That only explains why the joined tesseract is CRF, but does it explain it being regular? Well not quite, we need to do some more. Anyway, those square pyramids are flush meaning we get 24 octahedra, but how can we know its actually regular? Well, the 16 starting tesseract vertices are obviously the same, since the operation maintains symmetry, but what about the 8 new vertices? How are those the same? When you join a polytope, the vertex figure at the original vertices becomes a joined version of itself, and because the tesseract's vertex figure is the 3-demicube, joining it just gives you cubes. And obviously the 8 new pyramid vertices have cubic vertex figures since they're cubic pyramids, and voila! We proved that every vertex of the 24-cell has a cubic vertex figure. The most pedantic and annoying among you will notice that we didn't actually prove that the 24-cell is vertex transitive, just that it has the same vertex figure everywhere.
And I'm gonna be real with you: I don't know how to prove that. This is good enough for me. Also, it's not vertex transitive. We've been defining it relative to the tesseract, so its symmetry group is still B4, which, ico is not vertex transitive under B4 (in this orientation. In the rectified 16-cell orientation, it is vertex transitive). You need to, in a sense, triple the symmetry group to get F4, then its vertex transitive.
There's also some non 24-cell reasons that the 4-cube is my favorite n-cube. Mainly that it has 2 rings of cubes, and the diagonal being of length 2 thing is cool on its own. Not a whole lot, but yeah. I actually like the 6-6 duoprism more than the tesseract, but that's just because the tesseract is so talked about it's boring. Trying to remain logical here, for some reason. Honestly, I don't even like the tesseract that much at all. Why did I even put this here? Whatever, I said some cool stuff I don't want to delete, so it's staying on here. I've been working on this page for too long I need to publish it now.
8th - Bowtie

My favorite semi-uniform polytope, the bowtie! This thing is cool for a few reasons. It's the only non wythoffian semi uniform polygon, its vertices change direction on the circumcircle, and the angles vary with its proportions. My favorite proportions are pictured above, 1 and √2. This is because it puts it in the square army. It has facets passing through the center, making it a hemipolygon, meaning it doesn't have a dual. Honestly that's all I have to say about it.
7th - 3 Snub 24-Cell

If you cut back half of the vertices of a uniform or regular polytope with a 2-colorable edge graph as far as they'll go, you get what's known as the alternation of that polytope. If it is possible to then morph the elements around until you get a uniform polytope, that's called a snub polytope! If it's already uniform, then it's not snub. Which is kind of weird, but, calling demicubes snub feels weirder. Also if they have a coxeter diagram with snub nodes, that makes them snub too, if they're not already snub by the first definition.
The 3 snub 24-cell is, as the name implies, the uniform version of the alternation of the truncated 24-cell. All of its truncated octahedra alternate to non uniform icosahedra and tetrahedra, and all of its cubes alternate to tetrahedra. This shape is very cool to me. I used to think it was the only Archimedean snub that's not an alternation of an omnitruncate, but it's actually the alternation of the D4 omnitruncate.
I love how it has icosahedra. That's really uncommon. It's also one of the 3 (of 41!!) 4D Archimedean solids to only have regular facets! The other 2 being the 2 op 5-cell and 2 op 600-cell. The icosahedra also connect in a cool way, forming a hexagon.
This uniform polychoron has F4/2 symmetry, but it's not chiral. This is interesting to me. I've played around with the shape and realized that it's not chiral because of the more degrees of freedom 4D has. A 3D version of this solid, if it were to exist, would probably be chiral. But that's just a vibey thing.
Update: MinersHaven has told me that this thing does have a few 3D analogs! Most directly, the omnisnub demicube, which in 3D is the snub tetrahedron. Which, when uniform is an icosahedron, but when non uniform IS chiral, so I was right! Also, I have an explanation as to why this thing isn't chiral, despite being snub. It's because it's 4D!

Look at this picture of the 3 snub 24-cell. Looks pretty chiral right? Well that's because we're centered on a face between two icosahedra. If this was a polyhedron, that'd be that, and it'd be chiral. But in 4D, faces can connect higher rank elements (cells). You can flip this triangle around 180 degrees, swapping the two icosahedra, and you get the opposite "chirality" in the image. So yeah, that's how it's not chiral! Because the triangular faces can reflect, due to the more degrees of freedom of 4D.
This polytope is one of 4 non wythoffian Archimedeans. The other 3 are the snub cube, snub dodecahedron, and the deditdex. The deditdex has a spot on this list, actually!
One last thing I'll mention is that this shape is a diminishing of the 600-cell based on the vertices of an inscribed 24-cell! That's really cool to me. Anyway, I like this shape quite a bit, but it's kinda ugly and is on basically the same level as snic and snid, so that's why it's so low on this list.
6th - 16-Cell

Once again, I'm picking one shape out of an infinite family. I have a reason!!! The 4-orthoplex (fourthoplex for short) is the only orthoplex to also be a demicube. Unless you count the 1-orthoplex, which I don't, because the 2-demicube is 2 edges degeneratively on top of each other and is a different rank. The fourthoplex is also the 4-demicube because the orthoplex is the previous simplex antiprism, and the previous simplex (tetrahedron) is a demicube, and the demicube is the previous demicubeic antiprism.
This fact allows the 24-cell (or more accurately F4) to exist. I'll explain: take a compound of two opposing 16-cells, and this would have B4 symmetry. Its components would only have D4 symmetry though, even though individually, not in a compound, they have B4 symmetry. But hold on, if we have two fourthoplices with their vertices inscribed in a tesseract, then we can place a third fourthoplex, dual to that tesseract army! And that makes the compound of 3 16-cells, also called a stellated 24-cell.
For any dimension n where the n-orthoplex and n-demicube are equivalent, Fn exists. This is only true when n ∈ {0, 4}.
Anyway, the 16-cell is SO COOL!! It makes the 24-cell, and is best friends with its dual the tesseract, but also, it tiles space! It has a dihedral angle of 120 degrees. Anyway, yeah, the 16-cell is my favorite orthoplex. Octahedron is pretty cool too, for, you guessed it, 24-cell related reasons.
5th - Deditdex




The deditdex is very cool, it's basically what you get when you carve off 2 perpendicular rings of 10 vertices from the 600-cell to get a shape with 20 pentagonal antiprisms and god knows how many tetrahedra (I forgot and don't want to look it up). This shape's existence is part of why I like H4 so much, and the ring of 10 vertices is heavily related to the stuff I say about H4 in second place.
I'll try not to talk about H4, even though I love it, because this section is about the deditdex! I love how it highlights that rings can be perpendicular in 4D, with its two rings of paps. Also, it's the only non wythoffian non snub Archimedean solid! This is EXTREMELY significant. In all of math, there's only one non wythoffian non snub Archimedean, and it's comprehensible! It's more complex than ico, but, it's still only four dimensional, so it's relatively easy for a human to comprehend with a few months of practice.
The deditdex is non wythoffian, meaning it's not some simple operation applied to a platonic solid, or a shape generated by mirrors and reflections. But it's also non snub, meaning it isn't the result of kneading the vertices of an alternated uniform polytope into another uniform polytope. There are 3 other non wythoffian Archimedeans, and I discussed them in detail in the 3 snub 24-cell's section.
Edit, 1/16/2026: after a conversation on the polytope discord, and poll, I have learned that most people consider the deditdex snub. I don't really get it, and I disagree, but I thought it'd be dishonest for me to not mention this, and that my definition of snub is a bit unusual. They mentioned some examples of polytopes that my definition would include/exclude, and honestly I'm not sure if those polytopes should or shouldn't be snub.
Regardless of if the deditdex is snub or not, it is still the most unique of the 4 non wythoffian Archimedeans, because of its symmetry.
4th - 6 op 24-Cell



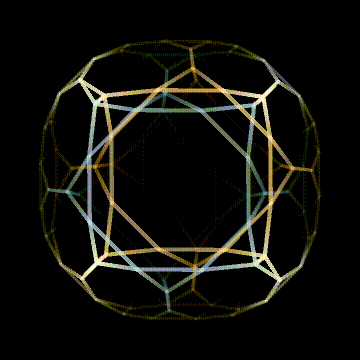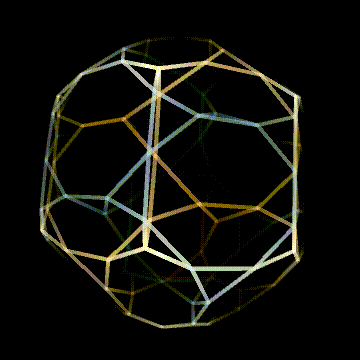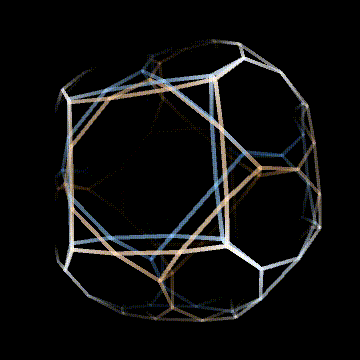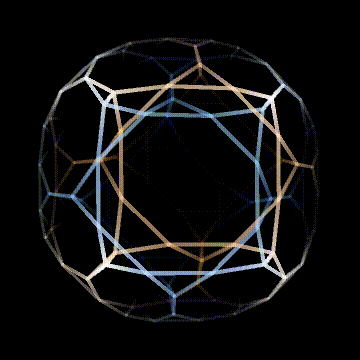

This is an Archimedean solid in 4D with F4⨯2 symmetry. This is because the vertices of the 24-cell turn to truncated cubes, and the cells of the 24-cell turn to truncated cubes as well. This means that the vertices now map onto the cells because the 24-cell is self dual. This is what doubles the symmetry group. I think this is really cool! There are only 3 Archimedean solids with F4⨯2 symmetry, the 9 op (expanded) 24-cell, the 15 op (omnitruncated) 24-cell, and the 6 op (bitruncated) 24-cell.
This may seem a little arbitrary, and it is, but F4⨯2 symmetry is very cool and the 6 op 24-cell has the fewest flag orbits of the 3, with just 3! That's why I'm including it here. Also, I think it's very pretty, and it's a noble Archimedean, which there are only 2 of in 4D. The other one being another 6 op of a self dual platonic solid, the 6 op pentachoron.
3rd - Hexelte-α (And En Polytopes As A Whole)




The hexelte is a uniform 6-polytope with 99 sides and 27 vertices. The 99 sides are split into two orbits of 27 5-orthoplices and 72 5-simplices. It has one of the most unique finite spherical symmetry groups ever, E6, only existing in dimensions 6-8, and having very erratic analogues. As for analogues of the shape itself, in 3D it's a triangular prism, in 4D it's a 2 op 5-cell, and in 5D it's a 5-demi. Very erratic indeed. The coolest thing about this is despite being an Archimedean solid not based on a platonic solid, it's wythoffian!
E6 is my favorite of the En symmetry groups. To be fair, it's the only one I kind of have a subjective feel for, as opposed to just understanding it logically, but yeah. E7 and E8 don't make sense to me because they have central inversion symmetry, and while they don't look like anything else I've ever seen before, they also don't look... new? I don't know how that works. I guess a better way to explain it is that I can't wrap my head around the 7 and 8 dimensionsal structure.
Okay right after writing that paragraph, I played around with a septelte-α in my program and gained more intuition about it ever before. I definitely don't understand it, but I don't have that weird thing about "how is it different but also I've never seen it before" anymore. It was so weird, how is it different from what? F4? Dn? Bn and An?? It's funny feeling like you're not sure what you mean whilst thinking it, rather than like, years after.
Anyway I still like E6 the best because it's the first, lacks central inversion symmetry, and the hexelte-γ is noble. I'm bundling the hexelte-α and hexelte-γ into the same chapter, but I like the α more so it gets the name and all but the last render.
2nd - 120-Cell



I love H4 symmetry. It's the prettiest of the 2 (or 3, depending on how you count) H class symmetry groups. I like it because it has vertices/facet axes with central inversion symmetry, as opposed to H3, where H2 and A2 both lack central inversion symmetry. This makes H4 have nice properties, like how the 120-cell has 12 rings of 10 dodecahedra. The 120-cell is very much a 4D decagon in appearance. They have the same dihedral angle and for an obvious reason: they're both facet transitive polytopes with rings of 10 facets! The gif I rendered shows off one of these rings very clearly.
I also love the 600-cell quite a bit, but not enough to get its own thing. Bundling the 120-cell and 600-cell into one makes sense I think. Also, the 120-cell is to be called the dodecacontachoron and this is a hill I will die on!
1st - 24-Cell




My number one favorite, the 24-cell! This shape is my favorite because it's the most unique platonic solid in any dimension. While it doesn't only exist in 4D, it is only regular in dimension n where n ∈ {0, 1, 2, 4}. (Assuming you generalize the 24-cell as a rectified orthoplex or joined cube) Its symmetry group, F4, is a tripling of B4, which is super cool! The only other B symmetry group to multiply at all is B2, which can be multiplied by any positive integer. (But only B2⨯2 makes a symmetry group in which B2 is a normal subgroup) B4⨯3=F4 is true, but, B4 is not a normal sub group in F4, which I don't fully understand, but I think in terms of what it means intuitively, the 3 groups aren't "perpendicular" in F4, so to speak.
Ultimately, I don't really care if B4 is a normal sub group in F4 or not. Since writing that paragraph I understand it a little better, and it's just about if transforming in B4 ways affects the other 2 B4 subgroups. So, saying normal subgroups feel perpendicular is correct I think.
Anyway, there's lots I like about this shape. Mainly that it's so cubic. It has B3 vertices, and B3 facets. The Archimedeans based off of this shape are so pretty, because of the cubic symmetry the facets are much more symmetrical than normal. For example, when the cuboctahedron pops up, it is actually a rectified cube/octahedron! Usually, when a cuboctahedron comes up, it's an expanded tetrahedron. Which has half the symmetry of B3.
The tetrahexachoron is also the only non trivial self dual platonic solid, aka it's not a simplex or regular polygon. It's also the only platonic solid to have orthoplex facets, that are not also n-cube facets. (This is to exclude the 3-cube and n-gons). The icositetrachoron is really pretty too, I love how it emenates the vibe of the number 6, because it has central inversion symmetry (lots of it actually because all of F4's axes have central inversion symmetry) which makes it feel even, and then with the B4⨯3 thing, it feels divisible by 3. Also because it has triangular faces.
Also, while writing this page I reread miners' favorite shape page's* section on the 24-cell, he says the 24-cell is four more things I didn't realize it was: 4 op n-cube, 2 op n-demi, and their duals. Not particularly ground breaking, but, they didn't occur to me.
*His page was inspired by my original page, so it's fitting that I mention it in the new one.