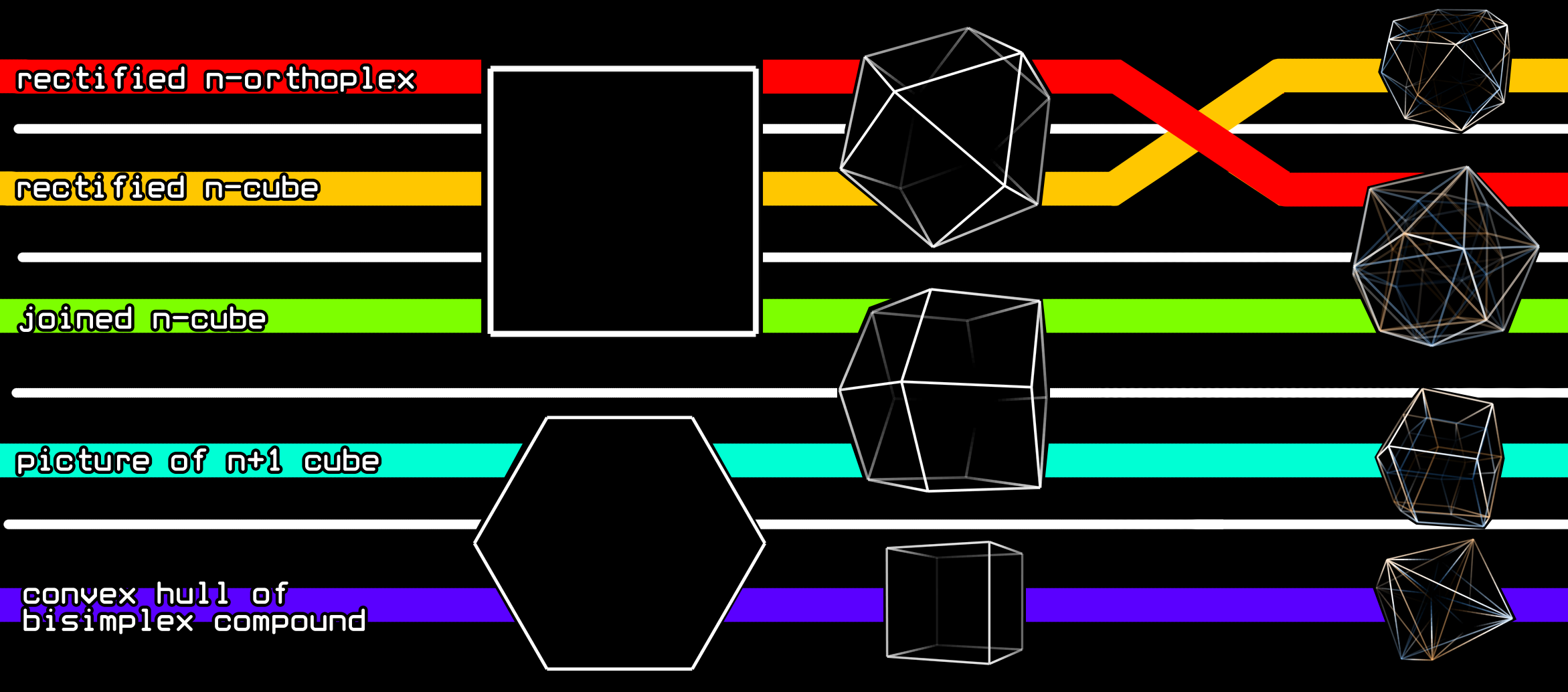
24-Cell Analogues In Other Dimensions

If you're a math nerd who uses the internet a lot there's a decent chance you know about the 4D platonic solids. There's also a good chance you remember the 24-cell, the 4D platonic solid that is often said to have no analogues in any other dimension. This myth has spread so far and wide, it's almost fact on the internet. I will show you how that's completely false, and the beauty of all the analogue chains that come with it.

This webpage assumes you already know some basic stuff about polytopes, and what the 24-cell is. Here's a quick recap: if you truncate a regular polytope really far, you get another regular polytope back with the same symmetry. These two polytopes are called "duals" of each other.

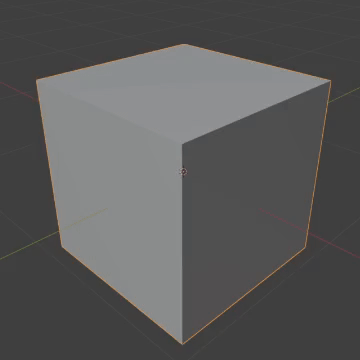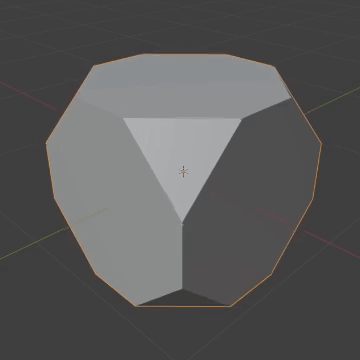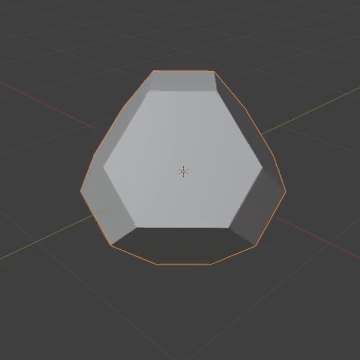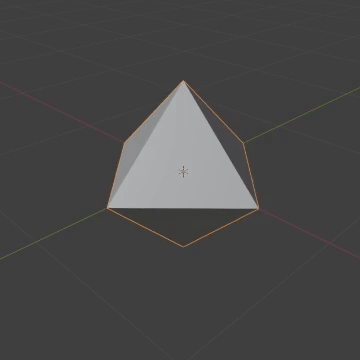
The 24-cell is a platonic solid in 4D that has octahedral sides and a cubic vertex figure, meaning 6 octahedra come together at a vertex in a cubic way. This might be a little weird if you're not used to 4D, but just remember that the surface here is 3D, so these octahedra really do fit.

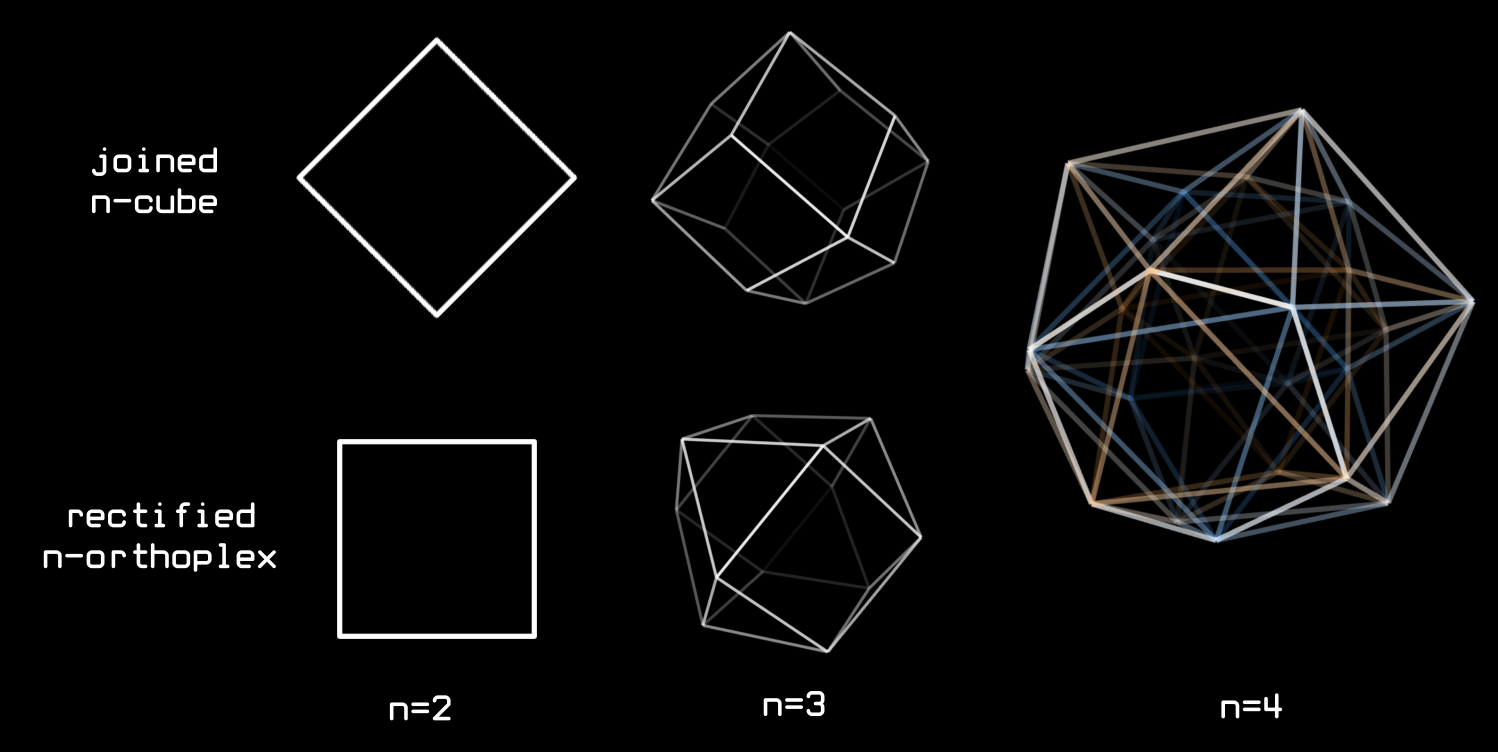
This 24-cell is actually the intersection of two n-dimensional sequences. The rectified n-orthoplex and the joined n-cube. An orthoplex is an n-dimensional polytope that is the bipyramid of the previous orthoplex. Okay, that sentence is dense, allow me to break it down for you. An n-dimensional polytope is simply a shape with flat sides that exists in every dimension, usually accompanied by a simple formula for its construction. And a bipyramid is when you use a shape as a base for a pyramid, but then like do it on both sides.

Rectification is when you cut the corners of a polytope far enough that the cut regions touch. So in 4D, if you rectify the orthoplex, you get the 24-cell. The 4-orthoplex is called the 16-cell, it has tetrahedral sides and an octahedral vertex figure. When you rectify a shape, all of its facets rectify, and its vertex figure is added to the polytope at every place where a vertex was. So for the 16-cell, that means we get 8 octahedra where the vertices were, and 16 rectified tetrahedra (which are also octahedra) where the cells were, which means 8+16 or 24 octahedra.

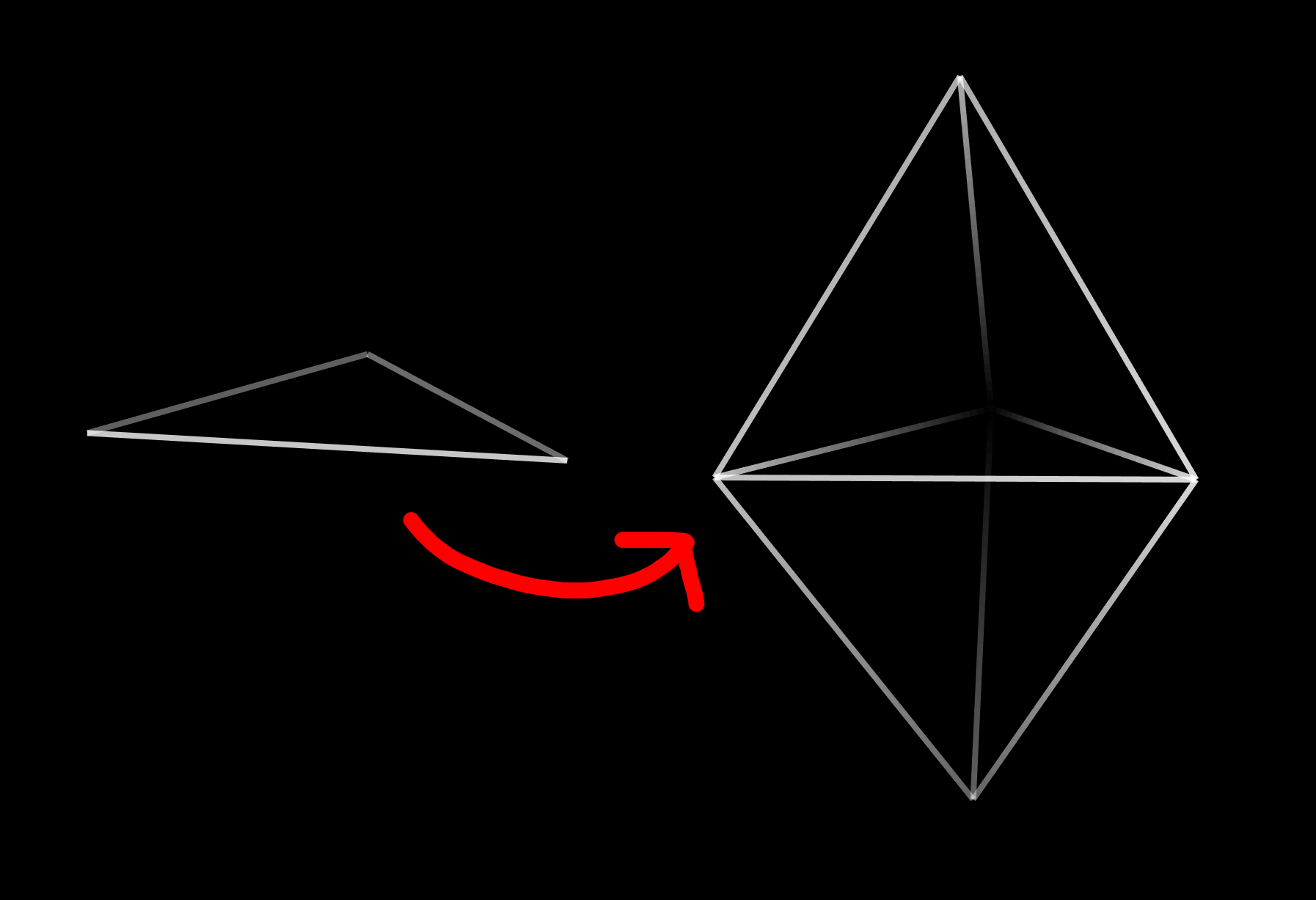
The other thing the 24-cell is is the joined tesseract. I really don't like the name “joined n-cube” but oh well. Here's how it works: Imagine placing a vertex at the center of the n-cube, and connecting every facet to the vertex. It is now made of pyramids. If we flip these inside out like this amazing wikipedia gif shows, we get a convex polytope that tiles space. This is a joined n-cube. If you look carefully, you might spot the cubic pyramids on the 24-cell, and the tesseract in the center here. Pretty cool right? The 24-cell picture (made by me) projects the cubes down nearly to squares, so those double square looking things are actually cubes, and so that big cube in the center there is the tesseract, and all the square pyramids are actually cubic pyramids.

GIF Credit

Let's look at more dimensions. In 2D, both of these are squares. In 3D, there's the cuboctahedron and rhombic dodecahedron, and in 4D, both are the 24-cell. Something neat is that in every dimension, the rectified orthoplex is dual to the joined n-cube, and in 4D this is still true, but the polytope is self dual. I think that's pretty interesting.

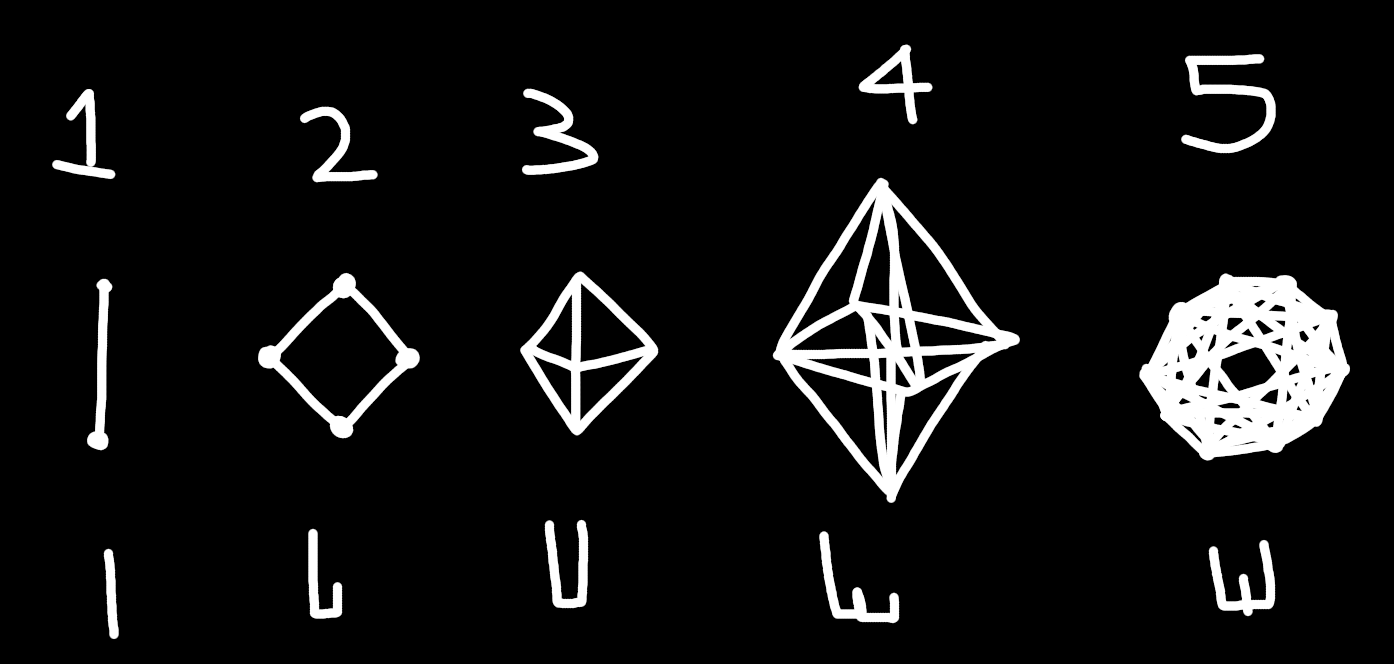
Now we know that the 24-cell is not only not unique to 4D, it actually is two n-dimensional shapes at once! Saying that the 24-cell is unique to 4D is extremely ignorant. However, the symmetry of the 24-cell is unique to 4D, as far as I am aware. This symmetry group is known as F4. But I want to go further. If the 24-cell is two n-dimensional shapes at once, maybe some of the other shapes on the chart appear in other sequences too.

The rhombic dodecahedron is also the vertex first orthographic projection of the n+1-cube. In 2D, that gives us the hexagon, and in 4D, this gives us the triangular antitegmatic icosachoron. Fun fact about this n-dimensional sequence: it tiles in every dimension, and makes a fair die in every dimension, since it's always a convex isotopal polytope with central symmetry.

In order: Vertex first projection of tesseract (rhombic dodecahedron), hexagon, icosachoron

The cuboctahedron is also the rectified n-cube. In 3D, if shapes a and b are duals, rectified a is equivalent to rectified b, and the n-cube and n-orthoplex are always duals. In 4D and beyond, rectification does not create the same thing for duals. This is the rectified tesseract, check it out! It looks very cuboctahedral.

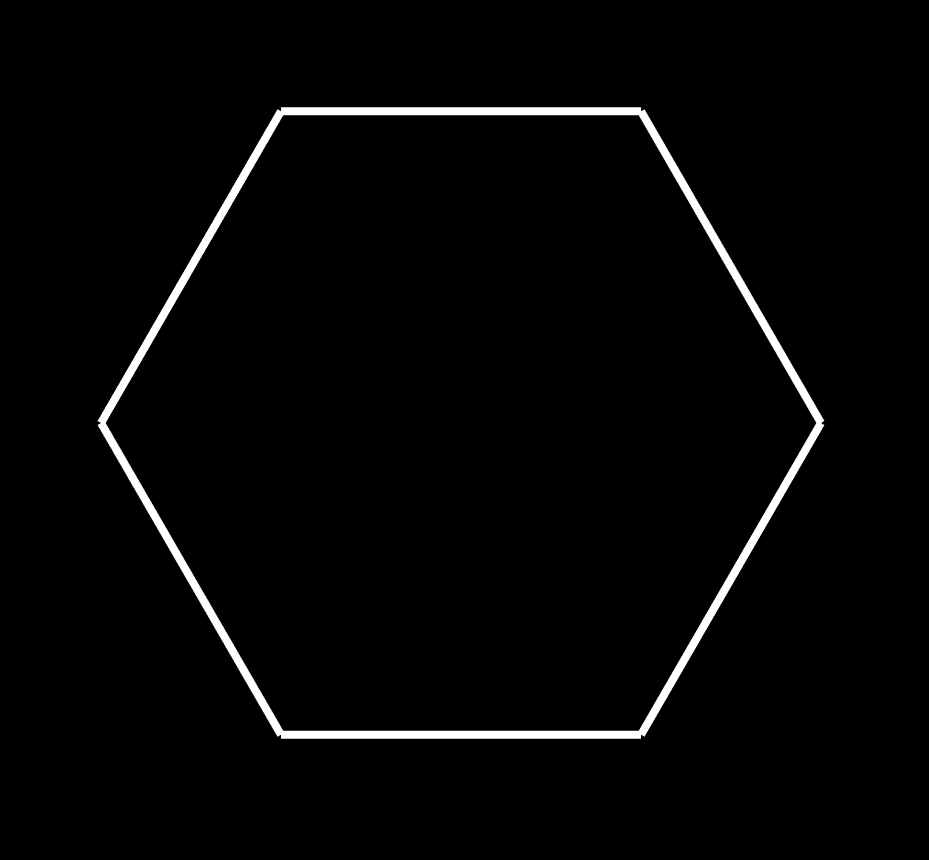
Finally, we have the hexagon. What else could it be? It's the convex hull of the compound of two simplicies, duh! (joke) That sentence is also very dense, so I will break it down: A simplex is an n-dimensional polytope that is the pyramid of the last simplex, so it goes triangle, tetrahedron, pentachoron, and so forth. In every dimension, the simplex is the simplest polytope by facet/vertex count, hence the name. It's also self dual. So if you have a simplex and its dual, you get a very symmetrical arrangement that works in every dimension. Finally, if you shrink wrap this shape, you get something known as the convex hull. The hexagon is this shape in 2D. In 3D, it's the cube, and in 4D, it's this thing!

The 2D and 3D cases show the original compound since your feeble human mind can construct the convex hull while looking at them easily, but the 4D case not so much, so the 4D picture is of the convex hull.

Another thing that I've neglected to mention is that we can not only take the convex hull, but the stellation core of these compounds. That still gives us the hexagon in 2D, but now the octahedron in 3D, and decachoron in 4D. This shape is the truncated triangle, rectified tetrahedron, bitruncated pentachoron, and so on. Whatever truncation like operation is exactly halfway between duals in dimension n, it's that one, applied to the simplex.

Also, fun fact: these convex cores are dual to the convex hull! That's simple enough to see with the hexagon, and cube and octahedron, but with the decachoron and bidecachoron it's harder to know. That's why they aren't on the chart, they're too far and they're just the duals so they're basically the same thing. There's no reason to prioritize convex hull over stellation core, I just thought of the convex hull first.

Here's the final chart. Well, that's about all I have for today. Thanks for reading. Don't spread misinformation on the internet.