I can visualize 4D space and you can too!
I often claim that I can "visualize 4D" or "think in four dimensions" a lot, but it's important to define the terms more precisely, so that I don't end up claiming that I can do something I can't. To clarify, when I say "visualize" I don't mean literally seeing a 4D object in all its glory like a 5D being would, or even a 3D image like a 4D being would. Remember, while you can think in three dimensions, you can only see two, and even in your mind's eye three perpendicular axes are impossible (at least for me) to see perfectly, without just projecting down and making the angles not 90. "Thinking in" a dimension means being able to do logic within it, and visualize means that you can figure out what stuff would look like there (even if it has to be processed down to a 2D image).
I just mean that, like the 3D framework built from just seeing as a baby, I have gained a rudimentary 4D visual framework, where I can imagine a 4D object or scene (but not actually view it) and then slice or project it to 3D, and then view that 2 dimensionally. It's actually kind of interesting, the 4D object (or some version/abstraction of it) really is in my mind's eye, but it cannot be viewed. It first needs to be processed down to 2D for me to view it. I know this framework is reasonably accurate, because like any good model, I can use it to predict things. Like predicting what a 7-3 duoprism should look like spinning on certain planes, then spinning it that way with my or other people's software, and seeing exactly what I predicted happen. Usually anyway, sometimes I'm a bit off and my ability is frustratingly inconsistent (especially when I'm tired), and since I don't use it super often anymore the skill began rusting.
In this webpage I hope to teach you how to build up the same! And I'll say that it's not very easy, it took me upwards of 4-6 months of nearly daily practice fueled by a special interest. Or it takes the average person a week, I don't know. Anyway if you really want to give it a try, I hope this resource will explain it well. Also, those 4-6 months were mostly spent going from 30/36 of the way to 35.8'3/36. Lastly, this webpage will cover the often neglected non geometric, natural 4D objects, like dogs, cars, and people! Without further ado...
Projection
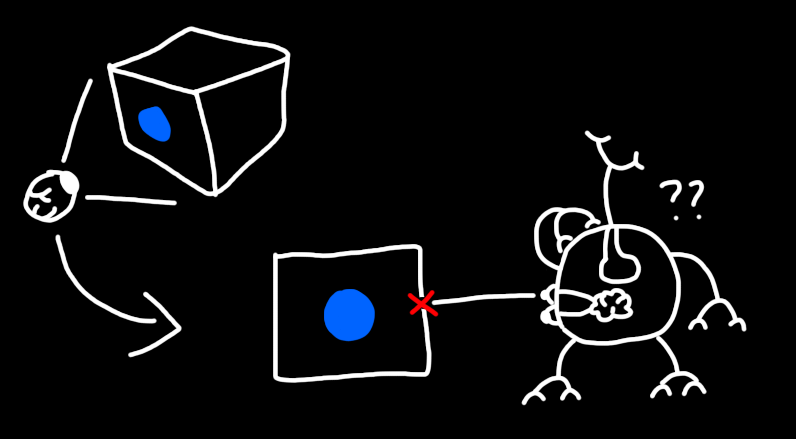
When we view an object, we can think of our eyes emitting a bunch of vision rays in different directions, and then reporting the color of the thing they hit back to our eyes. This isn't how it literally works, but optics is complicated and not necessary to know about right now.
In 4D it works the same, except now there's 3 angles that don't affect roll, so there's a 3 dimensional image to view. If you want more of an explanation, this image should explain:

Another way to think about it is that a 3D eyeball has a 2D surface, so our retinal image must be 2 dimensional. Likewise, a 4D eyeball would have a 3D surface, so the retinal image must be 3 dimensional as well. This is actually why four dimensional spheres are called 3-spheres. I don't like this nomenclature, I find it clunky and unintuitive, despite knowing why it is that way.
You may be wondering how direction is distinct from rotation. Well, a rotation is very specific. if you point at the sky, your finger's direction is up, but obviously that's not specific enough. What angle (relative to north or something) is your palm facing? This is called the axis angle approach to rotation, where you have a direction/axis (defined as a point on the unit sphere), and then an angle you rotate around that axis. In 4D, there's a 3D rotation perpendicular to that axis, and since 3D rotation is described with 3 numbers and a 4D sphere has a 3D surface, 3 + 3 = 6. There are 6 planes to rotate on in euler style rotation.
I'm not sure if I explained that very well, but this side tangent is over. Back to the point: 4D beings (with eyes) can see 3D images. These 3D images can't be viewed by us directly, but by making them semi-transparent we can render them just like any other object. Or, as this is about visualizing stuff in our mind's eye, we can do it there too. Let's start with something simple, a tesseract!
If we look at the front cell (cells are the 3D sides of a 4D+ shape) straight on, we see only the cube, as the other 7 are hidden behind it. To imagine what a 4D creature sees, just imagine a semi-transparent cube. It matters that its semi-transparent because the surface of the cube is not what matters, the inside does.
Imagine a black cube, with a blue dot on one of its faces. If we look at that face straight on, the other 5 faces of the cube are obscured. A 2D creature could imagine this picture as a blue circle contained in a solid black square. If they didn't make the square semi transparent, they wouldn't be able to see the "inside" of the square. This is why we imagine the cube as semi transparent. The "inside" of the cube is really the center, and you need to learn to think about surfaces as 3 dimensional.
Okay, now that you've visualized one extremely simple view of the tesseract, let's take things up a notch. Imagine a blue sphere is drawn on the tesseract's front cell, and then another black sphere smaller on top of that. (Remember that the tesseract's default color is black, so this appears as a hole in the blue dot) Even though this is an entirely 3D problem, you can feel how things are getting more complicated. Realize how a 4D creature, seeing this entire 3D image at once with no semi-transparency would be able to tell the difference between a sphere and a hollow sphere. Also, that they can see the inside* of this cube at all.
*this is not the inside of a cube, it's on the 3-surface of the cube.
Here's what that looks like, by the way. I know the sphere is a little lumpy, drawing in 3D is hard don't judge me!

I hope this gives you a somewhat intuitive feel for how a 4D being can peer inside 3D objects. Now, are you ready to actually peer into the fourth dimension? So far we've just been painting in 3 dimensions, but now we're going to actually think about 4 dimensional space! If you don't think you can make that leap, try out some more 3 dimensional images. Like a cube covered in dots, or a torus with a line through the center.
3D is Flat
The most important thing to learn is that 3D is flat, and 4D projection distorts 3D objects like 3D projection distorts the 2D objects making up 3D ones. Imagine a tesseract. It has 8 cubic cells, that come together at 90 degree angles. Let's rotate it 30 degrees to the right. If you're struggling to imagine what the 3D picture would look like, I will attempt to explain with a lower dimensional analogy.
If we rotate a cube to the right 30 degrees, the front face's left edge shrinks, its right edge grows, and the right face becomes visible. What is the higher dimensional version? Well, the left face of the cube shrinks, the right face grows, and the right cell becomes visible, with its right face very small. Try to imagine this on your own before scrolling down.
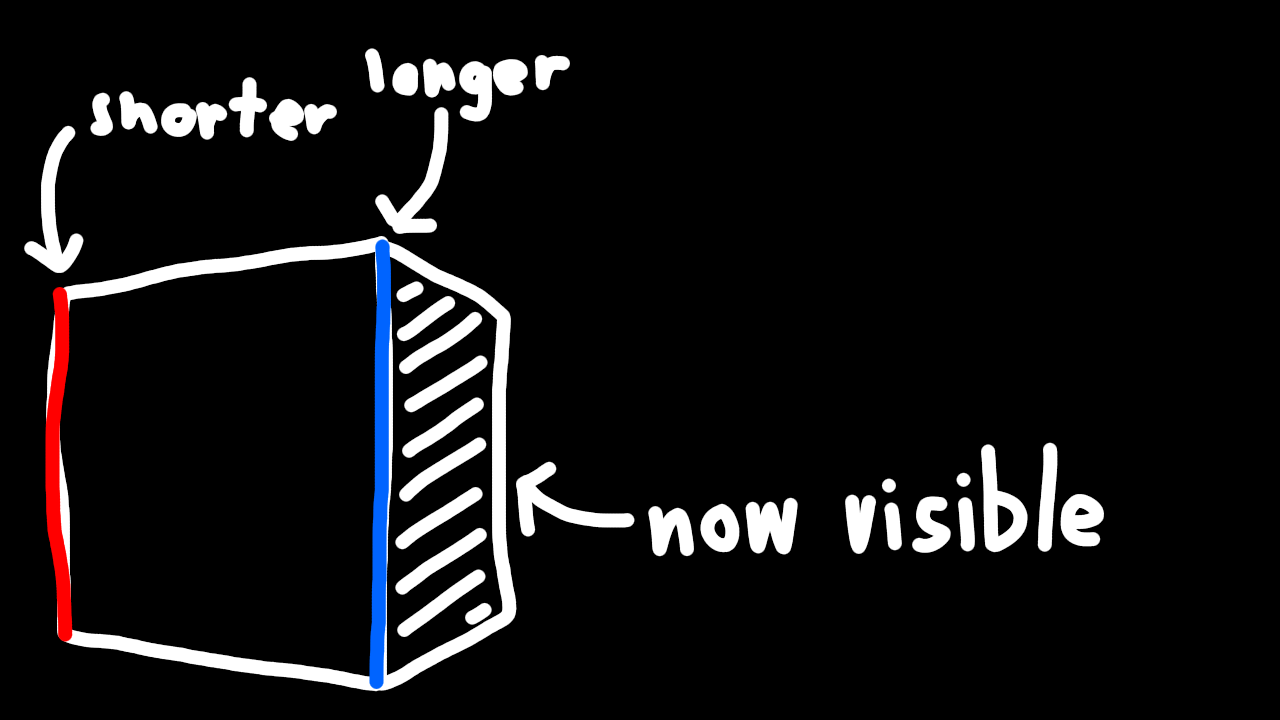

I've colored the right cell teal and the front cell orange. Something interesting is that from the front it looks like there are 3 cubes, a center one, and then two distorted square frustum ones. But in reality, the inner cube is just the back faces of the two other cubes. Makes sense, it's just like the "inner" cell of the tesseract gif being the back cell.

As you can hopefully see, 4D isn't really as complicated as you once might've thought! 3D shapes distort the same way 2D ones do, and they extend pretty intuitively. Interactive tools are also a great way to learn 4D. A lot of my 4D visualization ability is just me memorizing renders and then extrapolating patterns to other stuff. If I hear about a completely new 4D shape, unlike anything else I've discovered, it is considerably harder (but not totally impossible) to visualize.
Learning how to simplify a 4D scene or problem into a 3D one is very important. There's usually one axis you can ignore, at least temporarily. This may feel like cheating, but if it helps you navigate 4D better what does it matter? Finding what to rotate, where, and how to rotate it to simplify a problem isn't trivial! Especially if it's in your head.
For example, let's introduce 3 sides. So far, we've seen two sides of this tesseract. So let's rotate it up so that we can see 3 sides! From the front, again it looks like a mostly normal cube/tesseract, but now imagine what it would look like from the corner angle. Remember how we're trying to think about this as 3D just extended. Basically, as we've only rotated on two planes, it's just a rotated 3D cube extruded. Which extrusions are pretty simple!


Notice how on one of the axes, the shape doesn't change much. The colors combine in sort of confusing ways but remember it's still just red green and blue. Those are the only 3 cells visible. Actually, in the first picture, remember that the inner cube isn't really an inner cube, and is just the same cube but further away. This is what the second image rotates to reveal.
I know I promised some organic shapes, and so far this has all been geometry. Just two more and I'll try to explain how to visualize a four dimensional hyper labrador. So what I want to show you next is something TRULY four dimensional. So far everything has had very direct 3D analogies, or an axis can be ignored, simplifying the problem to three dimensions. But, if we rotate on a THIRD plane, now the RGB cube rotates partially out of view and we can see 4 sides, which is the maximum number of sides we can see on a tesseract at once. Without doing weird stuff like being inside of it, anyway. Which actually isn't that weird, that's how rooms work.
Anyway, I'll do my best to describe this. Let's imagine an orthographic view for now to make things simple. Imagine a picture of a cube, where you can see 3 sides. It can be orthographic or perspective, doesn't matter. It should have a vaguely hexagonal outline though. If you make it perfeclty aligned, it will be a regular hexagon. This makes it significantly easier to imagine, but also a bit more boring. Color the three distorted squares different colors in your mind, and now stop thinking of this shape as 3 dimensional. Think of it as a 2D shape or image. Now, extrude this shape upwards into a prism. It is composed of three differently colored quadrilateral prisms.
With me so far? Now, we're going to stop thinking of this as a 3D shape, and think about it as a 4D shape. Remembering that the top and bottom irregular hexagons are actually cubes, expand the top one vertically, so now it's a cube that's squashed on its diagonal by around half. This should distort the quadrilateral prisms its 3 bottom faces are connected to, and now, to make things even, distort the central bottom vertex where the three quads meet downwards.
If you're struggling about now, that's totally okay, I'm not great at explaining it and I'm literally trying to use natural language to explain a shape you're not programmed to comprehend. But, if you have all this in your mind's eye, keep it there. Just one more operation and you're done. Remember that bottom irregular hexagon? Take 3 of the 6 vertices (every other vertex), and make sure it's the 3 that don't bridge two quadrilaterals. As in, on either side of each selected vertex, its the same color.
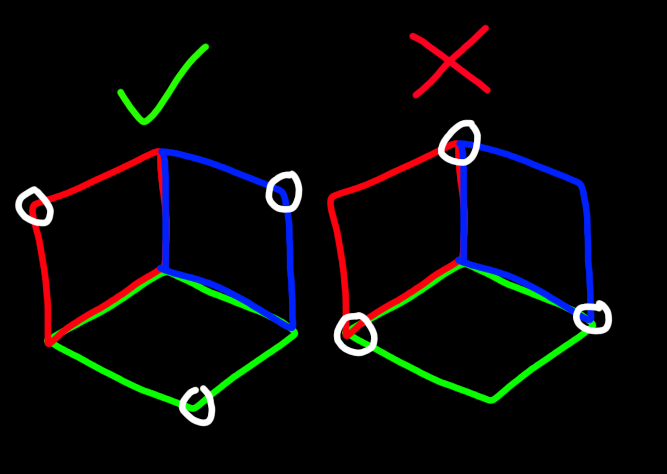
Grab these, and move them up a bit. Actually, if you did the thing with the revelead top cell correctly, you would have noticed that some vertices of the rhombus prisms had to move up to meet the cube, and some had to move down. This final operation just keeps those edge lengths the same and preserves the cube imprint on the other side.
Okay, well, if you followed all of that correctly... you should be seeing 4 foggy distorted cubes touching. Congratulations, without the help of a machine, you just visualized the 3 dimensional projection of the most complicated tesseract rotation possible! Notice that 4 cubes meet in the center to a vertex, this is the tetrahedral vertex figure of the tesseract. Now, here's the computer generated image. Put as a link as to not spoil it, if you want the challenge. I recommend trying to imagine what it looks like on your own, getting a real clear picture of it, and then clicking the link to see if you were correct.
Most likely, they won't look very similar, and that's just because taking a good screenshot of this 3D image is HARD. Your mental image is probably fine. Tesseract!!
Take a moment to be proud of yourself, that was no easy feat! Especially if you can spin that around now.
4-Ball
One more geometric figure before the hyper dog. The hypersphere! Let's start with something very simple, just a blank white hypersphere. A picture of this object would just be a sphere, so imagine a semi-transparent white ball. This is obviously a bit boring. Let's do what we did last time, and try to extrapolate from 3D patterns. If we have a 3D ball, we can put an ugly distorted square grid on it, like so. Image credit

We can notice a few things, but the main thing to notice is that the center of the sphere is the least distorted, and the edges are the most distorted. This is because of the normal, as the normal gets closer to perpendicular to your viewing direction, more of the surface is tilted away from you, making it shorter while still containing the same amount of space, which makes it compressed.
So now, extrapolating this up, the center of the hypersphere picture will be relatively flat, so just put 8 slightly stretched outward cubes (2x2x2) in the center of your sphere. Now continue that tiling outward, putting more and more cubes towards the boundary, getting smaller on the axis between them and the center of the image, and more distorted. This is a little tricky, but it doesn't have to be perfect. Just remember the general idea that as the hypersphere rotates, things move around inside that sphere and get squished towards the edge. Except the edge isn't an edge, it's a 2 dimensional surface boundary. A screenshot wouldn't do this thing justice, so here's a quick video I recorded showing the longitude latitude tiling on a hypersphere.
That might be a little too hard. Let's start by drawing a wireframe cube on the surface of a hypersphere! All you gotta do is imagine a semi-transparent black sphere with a white wireframe cube in the center with its edges bowed outward slightly. The curvature is not from the cube but from the surface it's on, S3. Next, rotate the hypersphere. All this means is moving the wireframe cube in a direction, and having it get thinner in that direction.


Four Dimensional Hyper Dog
I'm going to attempt to explain how I go about imagining the 4D equivalent of any object, or really just a specific photo in this case. The picture we'll be attempting to four dimensionalize is this one, that I got from google images. The first thing to do is start with the simplest elements, which is the background. We can ignore the top part, and just pretend the grass extends infinitely. Which of course we can just imagine as a green cuboid of random noise and lines, that gets higher frequency and more blurred towards the top of the cuboid.

If you really want to imagine the trees and stuff, uh, that's left as an exercise for the reader. Next let's look at the dog. The fun part about this is that I don't posess the skill to model a 4D dog in my raytracer engine, so you're just going to have to imagine it. First, I'm going to be using my generic octopodal extension of the quadropedal form. Basically having a leg at every vertex of a cuboid, instead of having a leg at every vertex of a rectangle like in a 3D quadroped. We're also not gonna rotate this image in 4D at all.
This means that we have the 4 legs in the picture, and then we have the same 4 offset in the W axis. I've drawn where the legs of the animal touch the ground in 3D space, based on the rotation of the dog's back legs relative to their front, etc. Notice how the dog being centered on the W axis actually pushes the legs out of alignment, to no longer live on the same plane. Remember, the cuboid pictured here is flat and will be rotated to be almost 2D, and then shown on the ground plane of the 3D image. This is identical to how you might map out the leg arrangement of the dog in the picture as four points resembling a rectangle, rotated in a specific way, with the back edge being rotated slighly more, and slightly larger. This 2D shape is then rotated in 3D until it's almost 1 dimensional, and then the size of the points from projective distance shows the size of the legs. Why almost 1 dimensional? Well, the further legs are still higher on the image. The camera angle is slightly down. As such, the same will happen with our cuboid. The larger points have larger legs on top of them, and are slightly lower on the image.
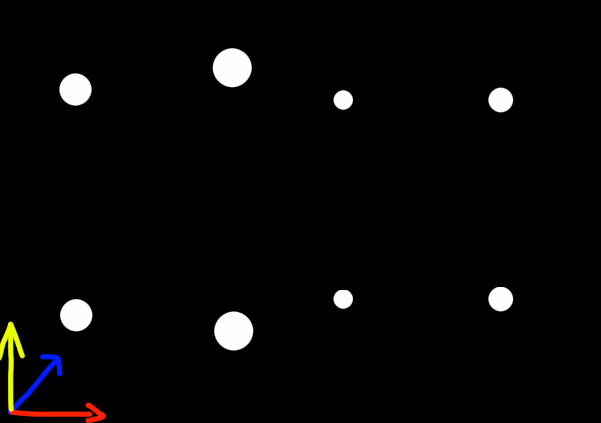
A quick tip for trying to visualize the 3D image of a 4D version of a scene, is to think about the picture as flat. Forget about depth and just see it as 2D, so you can understand how things relate to each other, with what's inside what. For example, see that spot on the bottom of the dog's chest that's in shadow? that would be in the center of the image, not visible from the outside (ignoring the fact that the grass also obscures the dog).
Next, let's 4D-ify the head! This is the most fun, as it has the most pattern extrapolation based pit falls. For example, you might be tempted to duplicate the two eyes, making four in a highly symmetrical square configuration. While I'd agree that this is the most aesthetically pleasing, it might not necessarily evolve. You only need two eyes for depth perception in every dimension. You could make an argument that nature cares about symmetry much more than saving cost, and yeah that may be a good point, I'm not an evolutionarily biologist. You can even imagine your hyper dog with 6 eyes in a regular hexagon! (Though, you should probably also give it a hexagon of front legs and back legs too, in that case. This is a very fun quadroped equivalent.)
The head of this dog at this angle looks like a very round triangle, which I'd turn 3D by smoothing out an upside down cone. Next, you can add the ears. The ears in the pictures are triangles that have been folded down at a strange angle. So I guess a 4D dog ear would be a cone (which is flat), and if you bend it down at a similar angle, you get a decently complicated shape.
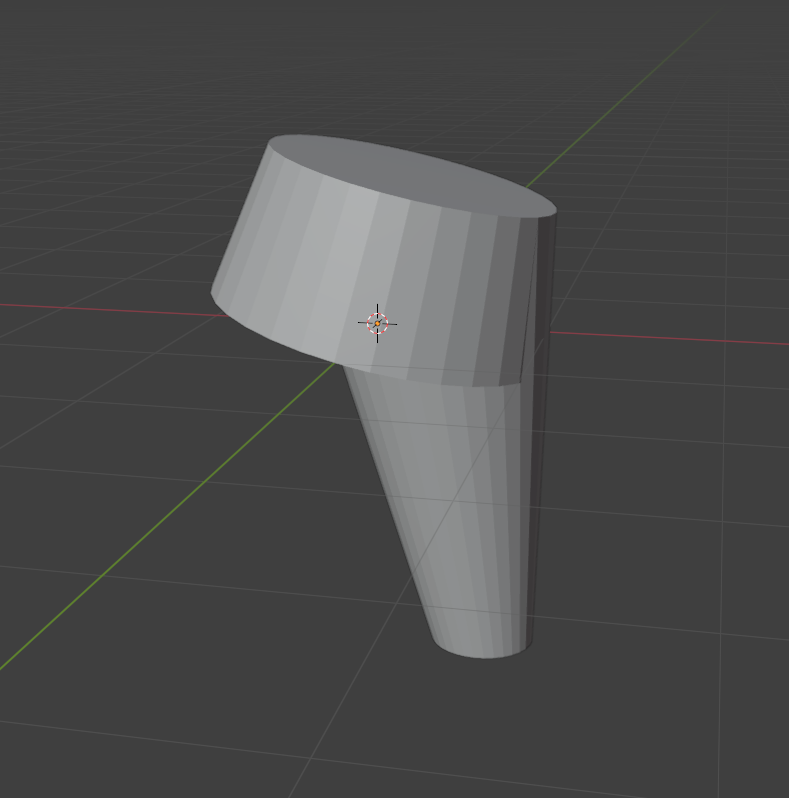
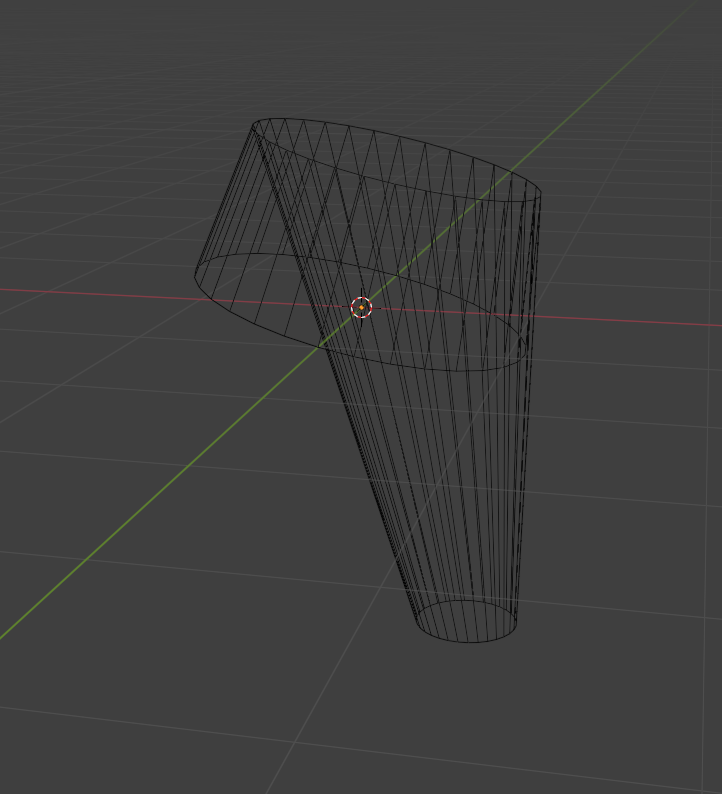
Obviously this doesn't look great, this isn't what it would actually look like, just kind of the vague shape/idea. I couldn't model the shape how I wanted in blender, but I'm sure you can see how something similar could look like the dog's ear. Dogs in 4D would probably have 3 or 4 ears. In order to know where a sound is coming from, you need at least n+1 ears where n is the number of dimensions. Up and down doesn't matter much, so we can use the n-1 dimensional space instead. But wait, you can see when the source of the sound is in front of you, and when you can't you know it's behind you, so that dimension also doesn't matter. So actually the n-2 dimensional space is all that matters. So the best ear arrangement for land dwelling n dimensional life forms is an n-2 dimensional simplex, arranged perpendicular to the up forward plane. So a line segment (an ear at each vertex) for a 3D creature, and a triangle (3 ears) for a 4D creature.
So that's why every animal has 2 ears. For the same reason 4D animals might have 4, 5, 6, etc eyes, 4D animals might have 4 ears for symmetry. But they only need 3. So imagine 3 or 4 ears placed radially on the head of the dog. Remember, the surface of the head is NOT the left/right/front/back of the head! We're looking at a 3D image of the dog, so those are the sides. The center of the head (like inside of it) is the front of the dog, where the eyes, nose, and mouth will go.
The dog's mouth would probably just be the revolution of the dog mouth shape from the image, so it would look like this. A 4D creature must have a 3 dimensional opening for a mouth, so that 4D food can enter. Finally, the nose would probably be a smoothed upside down square pyramid thingy, with 4 spherical nostrils. So just compile all of that into a 3D semi transparent object, the dog head shape, the ears, the eyes, the nose and the mouth.
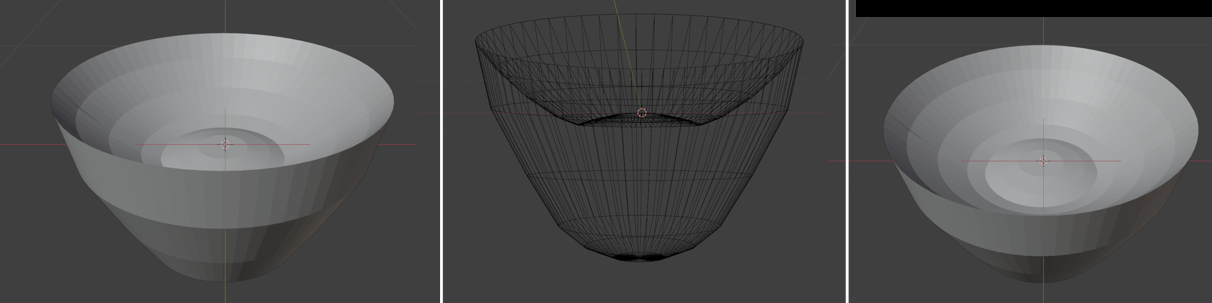
Explaining how and what to imagine is tricky, and imagining these 3D objects is tricky, so I hope this webpage is comprehensible and useful. I think compiling this into the full dog is pretty straight forward, get a blobby bean shape for the torso, (remembering to imagine a hair texture on the inside of it, that compresses towards the surface to give the effect of it curving away from you) Then you put the 8 legs in the cuboid arrangement, putting two of them in shadow. The tail is pretty simple, it's just a curve coming off the back. Then there's shadow on the lower parts of the torso, and under the head, and yeah if you can imagine all that we did it! 4D dog. I've been working on this webpage for far too long, so other smooth, natural, complicated shapes will have to wait on a part two, so that I can publish this.
This requires a lot of visualization effort, but with practice I hope you'll be able to get it. I really hope I didn't forget something, make an error in this, or explain this poorly. I hope you enjoyed reading this!