Anyone Reading This Who Likes Sports?

No takers? Haha I didn't expect any, this is a website for NERDS!! However, I think the soccer ball (football for my normal readers) is cool. Why? Well, it's based off the 3 op icosahedron, which is an incredibly round polytope made of round facets, and while it can't properly be 2-colored, it looks good enough.

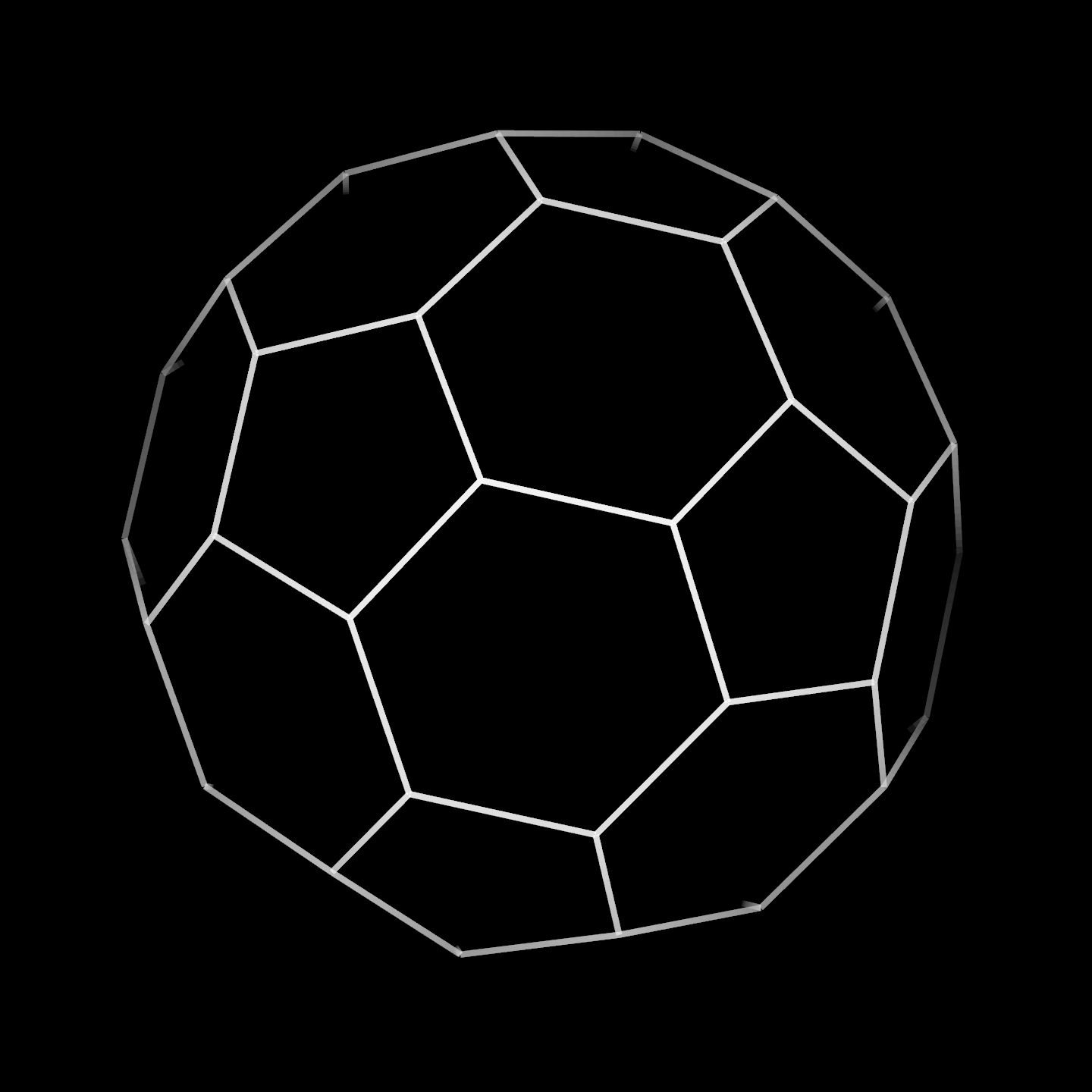
I think a polytope that is round, symmetrical, and has round facets is an interesting thing to try and find, so this webpage will document a bunch of higher dimensional soccerballs.

Other 3D Soccerballs

The 3 op icosahedron is the best 3D soccerball (in my subjective opinion), but there are other good ones. In order, from worst to best:

The 5 op dodecahedron is a polyhedron with 3 types of faces, so it looks weird when 2-colored. I think it makes sense to make the pentagons black, and make the squares and triangles white. Here's a picture of a real 5 op dodecahedron soccerball I found. It uses 3 colors, which I'm not a huge fan of.

The 2 op dodecahedron is a really cool looking and pretty quasi-regular solid. It makes a decent soccerball, but the triangles are a bit sharp.

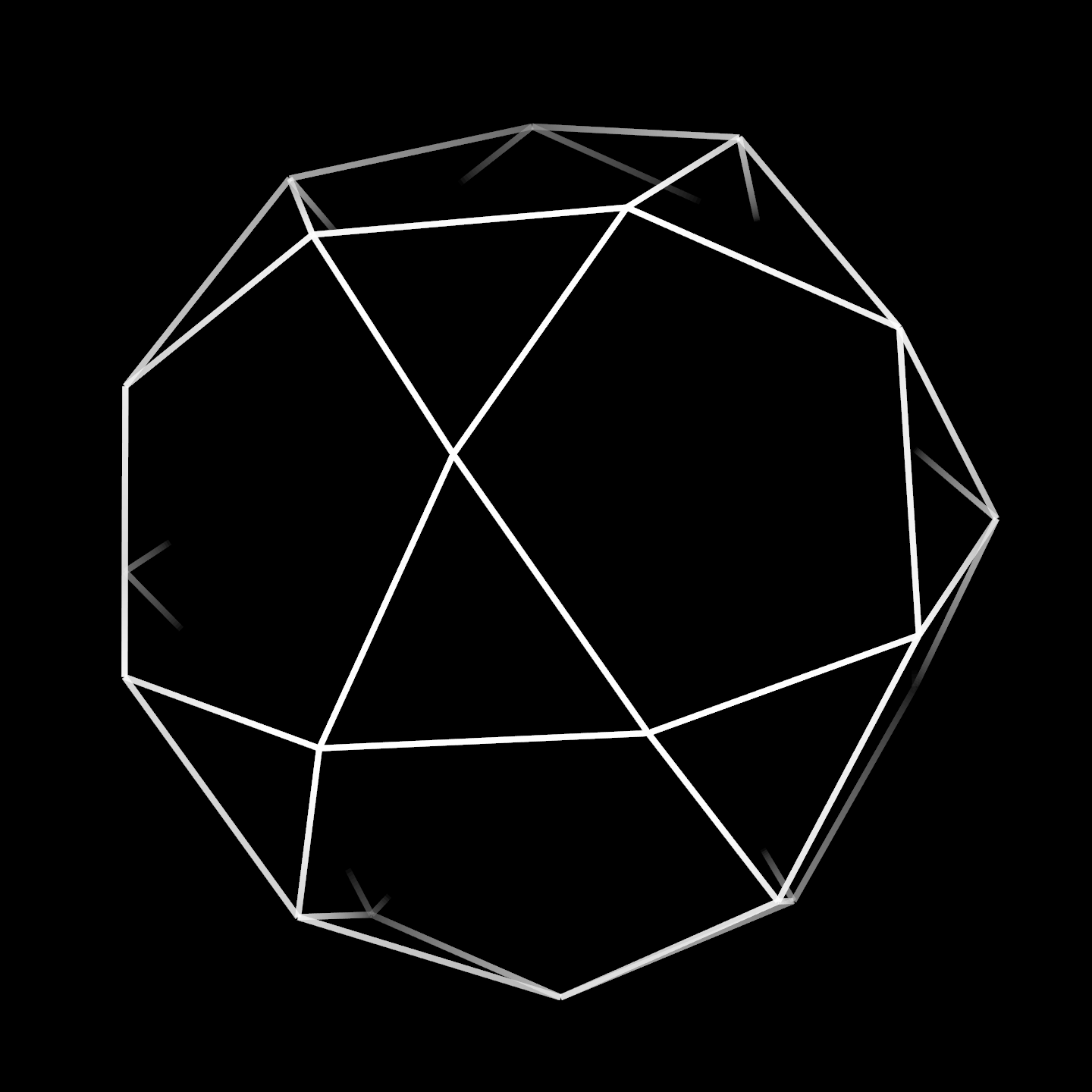
The snub dodecahedron is a really pretty and peculiar solid, and although it has a lot of triangles, they blend together in such a way where it appears pretty smooth, so I think it fits the criteria. If I were to color the faces, I'd make the pentagons black, and both types of triangles white. I couldn't find a real snub dodecahedral soccerball. If you find one please let me know.

2D Soccerballs

I think a 2D soccerball that makes sense is a white dodecagon with 4 black edges, each 2 edges apart. I have rendered what that would look like. This gif looks really bad and I don't know why. I think it's because it's dithered poorly. Not sure. Blame Kdenlive.

After making this I tried a 6 black 6 white variant, and I gotta say I like it more, but I don't want to record and trim and make sure it loops and then export again. Use your imagination.

4D Soccerballs

You might want to jump straight into trying to find an Archimedean, but, the 120-cell is plenty round, and so are its facets, and it has a nice coloring pattern using a 24-cell, so honestly it's pretty good. I was unable to make a picture of the coloring, so just take this vzome link instead.

There are a lot of other H4 Archimedeans that work as soccerballs, but I think the best of them is the 2 op 120-cell, followed by the 3 op 600-cell, and then there's the 6 op 120-cell/600-cell, which I don't see the appeal of, but I'd be remiss not to mention it. Here are their images, in order of mention:

Here's an interesting idea: a non H4 soccerball! I suggest the 9 op 24-cell. The octahedra should be colored black, and the triangular prisms should be colored white.

You could also use a 6 op 24-cell, and color half of the tics black and the other half white.

Lastly, you could use a 3 op 24-cell. It's not round enough in my opinion though. The 9 op 24-cell is probably the best of F4, and the 120-cell is the best of H4, and better than the 9 op 24-cell.

5D Soccerballs

Now here's the hardest dimension! 5D is a cursed dimension, it doesn't have anything cool or unique going on, besides the 5-demi, but that exists in literally every other dimension, it just only becomes prominent here. And besides, D5 has half the order of B5 by definition, so we don't care about it anyway.

That's not the cursed part though. The cursed part is that 5 is such a low number, and yet it's got nothing going on. At least 23D has an excuse for being so empty, it's a really high dimension so it's harder for unique things to happen, and everything is highly asymmetrical.

It took me a good hour or two of thinking, searching, and viewing, but I think I finally found one passable 5D soccerball. Behold, the 7 op 5-orthoplex! This thing has 3 types of facets. The 40 octahedral prisms shall be colored black. The rest will be white.

I chose this for a few reasons. One reason is that most of the facets are fairly round. Another is that it has few facet types, and a good size mixture for spots. Finally, I chose it because it was round. Its sharpest angle is between the 3 op 16-cells and the 7 op 5-cells through their 3 op tetrahedra, at 116.56 degrees. This isn't a great ball, but for 5D I'm pretty happy with it.

The 7 op 5-cells aren't easily visible in the image. Oh well.

6D, 7D, and 8D Soccerballs

6D, 7D, and 8D have been lumped together due to the existence of the En symmetry group, which exists in dimensions 2-8, but is only unique after 5.

Starting with 6D, my very first thought was to try the hexelte-γ, but it's not very round, being slightly less round than a hexagon.

It took me a long time to find anything good, but, I think I got it? Basically, start with an anti hexelte-γ. This thing has 120 degree dihedral angles everywhere, so it's just as round as a hexagon, I think, but it also has way sharper corners. To unsharpen those corners, just truncate it. The new semistellated 5-orthoplices should be colored black, and the truncated anti 4 op 5-simplices (note, the link is not truncated) should be white.

Unfortunately, I do not have an image of this polytope, but here's an anti hexelte-γ:

Finding a 6D soccerball was much harder than I thought. Let's try 7D now.

I think the 3 op septelte-α works well. The septelte-α is very icosahedral, so truncating it makes a lot of sense, as the 3D soccerball is a truncated icosahedron. Here are 2 gifs I rendered of it. The first one is a double rotation, XZ-YV, and the second one is staring at one of the hexelte-α facets, and double rotating in such a way that we keep looking at that one facet, and our camera doesn't roll. (XW-YV)

After finding this, I realized that the 3 op hexelte is another good 6D soccerball. Even though it's nicer in polytope terms, I think it makes a worse soccerball. I might update this page with an image of the 3 op hexelte in the future.

For 8D, I don't see any reason not to just use the 3 op octelte-α. The wiki is lacking an .off and I don't care enough to try and get one, so no image will be provided. :c

Higher Dimensions

For 9D and above, using the 7 op n-orthoplex is probably good, as that's what I used for 5D, and, I even put it in the 4D section, since the 3 op 24-cell is also the 7 op 16-cell! It's a lot better in 4D though, since the 3 op (truncation) of the octahedron and the 7 op (cantitruncation) of the tetrahedron are the same.

For even dimensions, you can also take the convex hull of multiple cartesian products of n/2 decagons. The decagons should be scaled so that, take 6D for example, one of the decagons is 1 + √2 times bigger than the other 2. This is to make the gaps the same size as the prisms. I probably explained that confusingly.

In 4D, you take two 10-10 duoprisms, and one of them is scaled XY, and one is scaled ZW, and then you take the convex hull of that. I don't know how to take convex hulls, but here's a picture to give you an idea. If viewed orthographically, it looks perfectly octagonal.

I think these look really cool. I love perpendicular rings. I'd make the rings black, or half of their components black, and the gaps filled by the convex hull white. If someone can get better renders of this, especially as an actually soccerball looking thing, please let me know so I can add it here. Actually, if anyone makes any better renders of any of these objects in the entire page, please let me know!

Conclusion

Polytopes are cool. This page has made it clear that 4D is the best, 3D is a little worse, 6D-8D are okay, and every other dimension sucks. 2D gets N/A. Thank you for reading this page, I hope you found it interesting and maybe even learned something from it. I definitely learned and had fun writing it. Didn't learn anything huge, just generally got more comfortable with certain shapes, and saw more uniforms that I don't often think about.