Regular Polytopes in 2-5 Dimensional Space
WARNING: This webpage is incredibly old! Meaning it does not meet my modern quality standards and has straight up incorrect information in it! I don't care about this page so if you find incorrect information I really don't care if you tell me or not. So yeah. Just thought I'd let you know.
What is a Regular Polytope?
A polytope is a shape that is defined by points, edges, faces, cells, and so on. They have all flat sides and no curvature. Shapes that aren't polytopes include: Cylinders, spheres, tori, etc. The word "polytope" is just the n-dimensional general variant of words like polygon, polyhedron, and polychoron. When a polytope is regular it means that it's vertex, edge, and so on transitive, and its facets are regular polytopes. I think mathematically speaking its impossible to make a fully transitive shape with an irregular polytope for sides, but it's also good for clarity to be water tight in your definitions.
This page was inspired by this amazing Jan Misali video. Here are my disclaimers to cover my ass because I technically don't include all the regular polytopes: This page describes (not contains, because of 2D's infinite regulars I can only describe them all) all regular polytopes in Euclidean space where a polytope is closed, finite, and that if two shapes look identical they are considered the same. If you want a more thorough explanation of all 48 known regular polyhedra, watch Jan Misali's video, it's great!
TLDR, I only include the "normal" shapes.
Schlafli Symbols
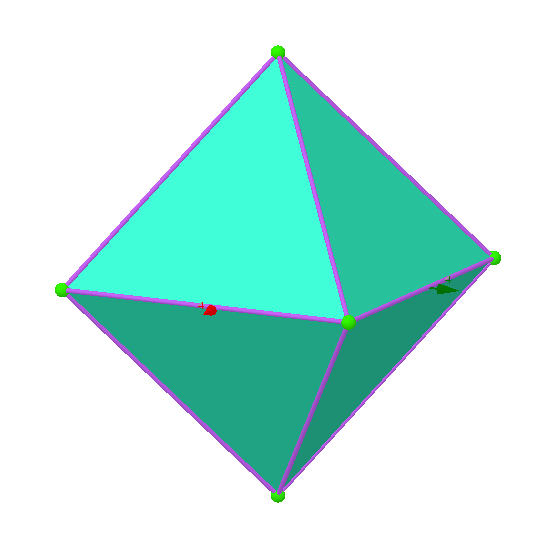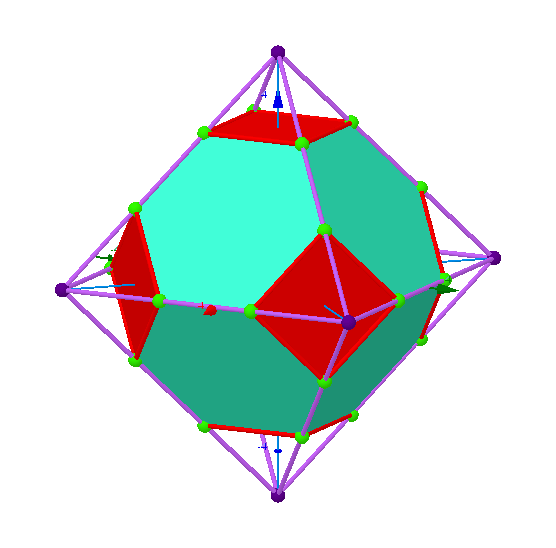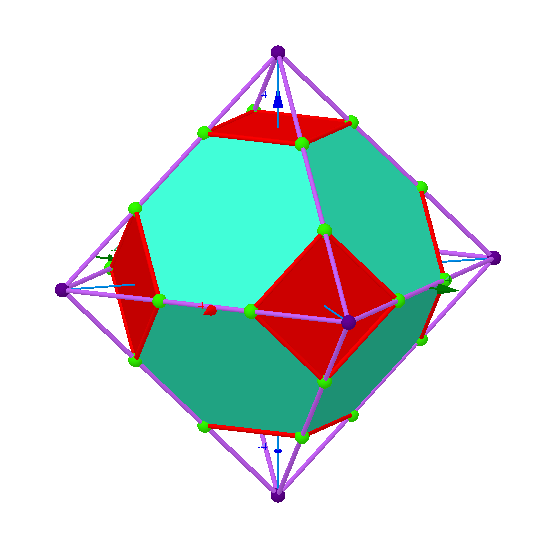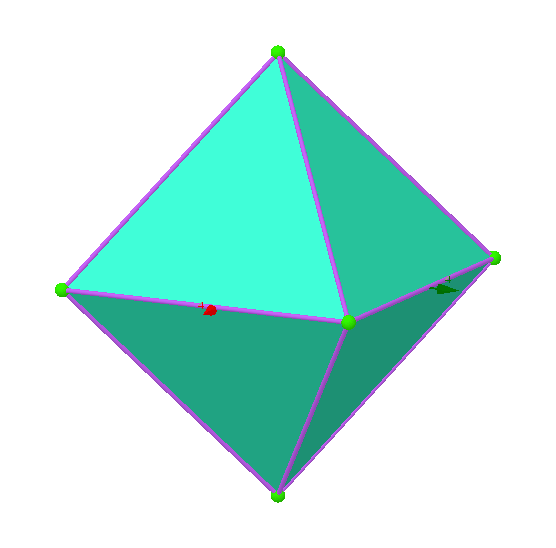
A Schlafli symbol is a great way to represent regular polytopes, as if you know the sides of the shape and the vertex figure, there's only one way to put them together. All numbers except the last are the side of the shape, and all numbers except the first is the vertex figure. The last number is how many sides meet at an n-3 component (n being the number of dimensions of the shape). I defined the Schlafli very weirdly so that it is an n-dimensional definition. So lets give some examples. A square is {4}. An octahedron is {3, 4} because 4 triangles meet at a vertex. It's good practice not to think of the numbers as numbers, but as polygons. So instead of 4 3 sided regular polygons meeting at a vertex, you can say that the triangle connects to other triangles with the vertex figure of the square. One more example. The 120-cell's Schlafli symbol is {5, 3, 3}. This means 3 pentagons connect at a vertex to form one side (regular dodecahedron), and those sides form together 3 at an edge. You can see that the vertex figure is {3, 3}, which is the tetrahedron. Below is a truncating octahedron and truncated 120-cell so you can see their vertex figures.

Two Dimensional Polytopes
Now that we have our terms defined we can move on to the fun part, the shapes! Starting with 2 dimensions. There are an infinite number of regular polygons. And this is one of the more boring infinities, where its infinite because there's a simple procedure you can use to generate any n>2 sided polygon. The way you do so is by placing n number of points on the surface of a circle with equal angular spacing. To connect these points with edges, we go from one to the next, stepping by one.

But what if we step more than one vertex at a time to connect edges? Well then we get stellated or star polygons. They look really cool, and are notated like this: {sides/step} The technical term is n, number of sides, and m, what I call step. So the pentagram, or stellated pentagon, is notated by {5/2}. And this is why it's important to think of the numbers as shapes, because what does 5/2 even mean? 2.5? Something cool is that it is kind of like division. If you were to treat it as an operation, if n is divisible by m then the polygon is a compound of m regular polygons with n/m sides. Like {8/2}, the stellated octagon. 8/2 = 4, and sure enough its a compound of two squares! Polygons that are close to this look kind of like optical illusions. Take {9/2} for example, it looks like two pentagons but its not, trippy!

Footnote: to calculate how many stellated polygons there are for any given polygon with side count n and step m, n/m can't equal 2 or lower, otherwise it becomes weird, or repeats ones that already happen at lower values, just inside out. The formula is: number_of_polygons = ceil(side_count / 2) - 1 This formula includes the convex polygon as one of the valid immersions of the polygon.
Three Dimensional Polytopes
Three dimensions, the space you're probably reading this from! If you're not, please get in touch. I'm gonna speedrun through this since I assume my target demographic is already familiar with these. So if we take triangles, we can fold them into a new shape in 3 different ways. 3 at a vertex, 4 at a vertex, and 5 at a vertex. This gives us the three regular deltahedrons. The tetrahedron, octahedron, and icosahedron. Fun facts about these: the tetrahedron is an edge anti prism and a triangular pyramid, the octahedron is a triangular anti prism, and the icosahedron is a gyro-elongated pentagonal bipyramid, which is also a bi-augmented pentagonal anti prism.

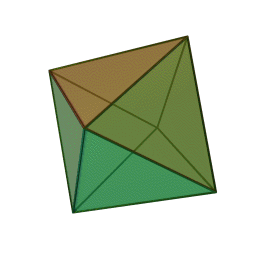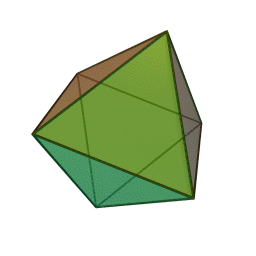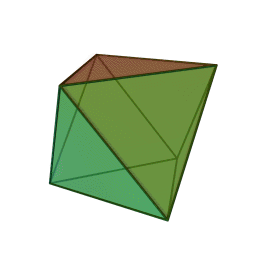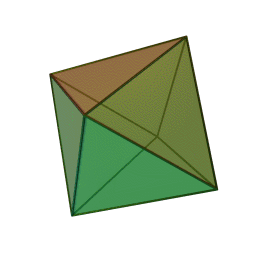
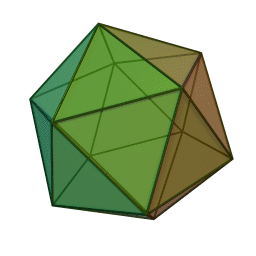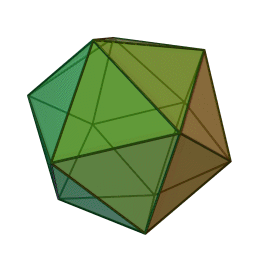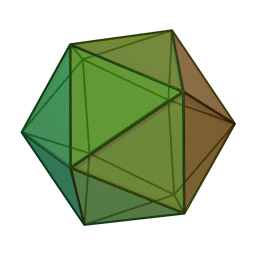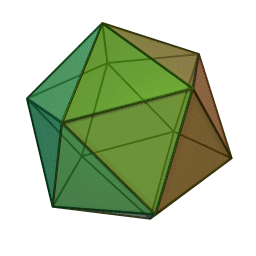
The next regular polygon is the square. We can only fold this one 3 at a vertex, and we get the humble cube. Next we go to pentagons and that also folds 3 at a vertex. We now have the dodecahedron, the fifth platonic solid in this ordering method. If we try hexagons, we get the hexagon tiling which can be thought of as a flat, infinite in size unclosed polyhedron but we're ignoring that. Take it up with Jan Misali.
The process of stellation is complex and I'll explain it after, so I'm going to ignore stellation in terms of spikifying shapes. Instead I will think about it in terms of folding shapes. We can use {5/2} as a face to make two new shapes, the small stellated dodecahedron and the great stellated dodecahedron. The first shape has a Schlafli symbol of {5/2, 5}, and the second has a Schlafli symbol of {5/2, 3}. The small stellated dodecahedron (left) is my personal favorite. As the names suggest, they both have 12 faces.


Next, rememeber when I said that Schlafli symbols should be thought of as shapes and not numbers? This is very important now, because we're now going to ask the question: What if we connect some shapes using a star polygon as a vertex figure? The answer is the last two stellated polyhedra. (Also called Kepler-Poinsot polyhedra for history reasons.) These two new shapes are: The great icosahedron, a shape with 20 triangular faces connected by the pentagram {3, 5/2}. The great dodecahedron, a shape with 12 pentagonal faces connected by a pentagram. {5, 5/2}. Wow, the great icosahedron and small stellated dodecahedron look so similar.

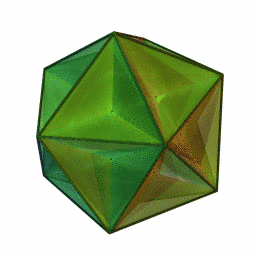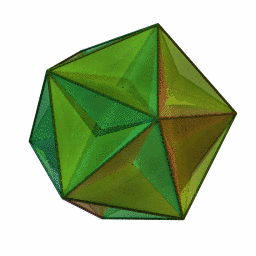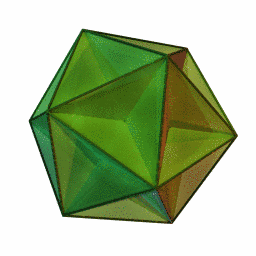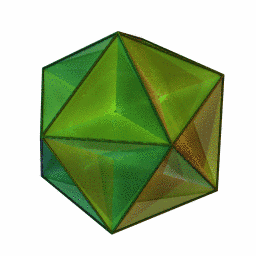
You may notice a symmetry between these four shapes. The first pair had pentagrammal sides, and the second pair had pentagrammal vertex figures, the first pair had pentagonal and triangular vertex figures, and the second pair had pentagonal and triangular sides! That is a concept called duals. If you flip a schlafli symbol, you get a new shape with the same symmetries, but the vertices and facets have swapped. Below are two gifs of the shapes transitioning between duals.


3D Stellation
There are two types of stellation. Greatening is the process of scaling up all faces until they meet into a solid polyhedron again, and stellation is when you scale all the edges until they meet. Then you can replace the faces with stellated counter parts that are stellated in the same way. Here's a handy chart I found on wikipedia.
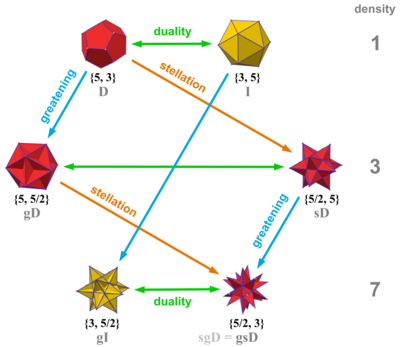
3D Compounds
Now, you've probably been told that's all there is but there are more! 5 more actually. My rules don't exclude compounds, and there are 5 regular compounds. If you were sad that there was only one stellation of the icosahedron like I was, this should make up for it. First one I'm talking about is the stellated octahedron, or stella octangula! Jan Misali didn't forget to include it, his rules claim that all shapes must be one continuous shape, and the stella octangula is two shapes in a trench coat. But this is my webpage, and my rules allow it! I think this is a really cool shape, and it is completely regular. You'd have to change your definition of regular to specifically exclude it. Its convex hull (the shape formed by their vertices) is a cube, which I guess makes sense as the cube and octahedron are duals. Also, the tetrahedron is the demi-cube, so of course two of them would make a cube.

The second and third regular compound are of 5 and 10 tetrahedra respectively. They are both stellations of the icosahedron, and their convex hulls are dodecahedra.


The fourth compound is of five cubes, and is a stellation of the "rhombictriacontahedron". Whoof, what a mouthful! That's 8 syllables! Its convex hull is the dodecahedron.


The fifth compound is of five octahedra. It's a stellated icosahedron and its convex hull is the icosidodecahedron, not a dodecahedron. The fourth and fifth compound are duals.
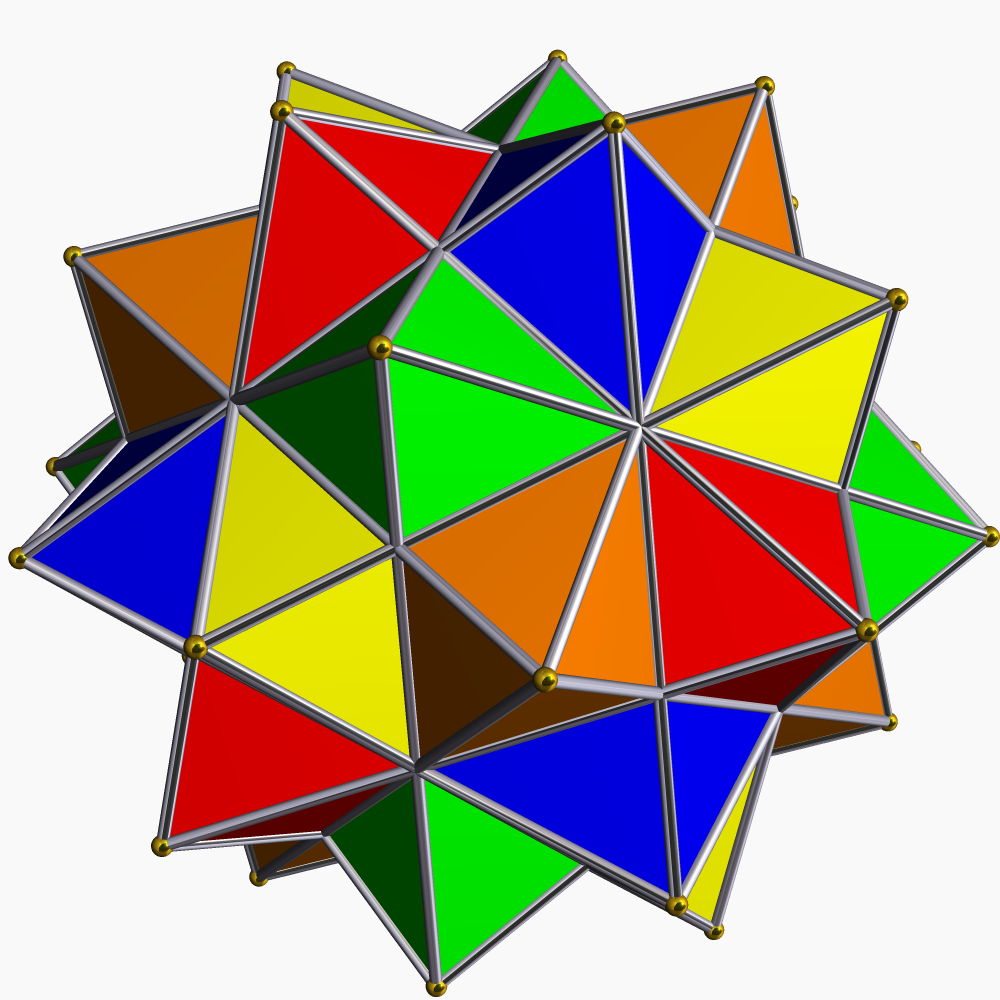
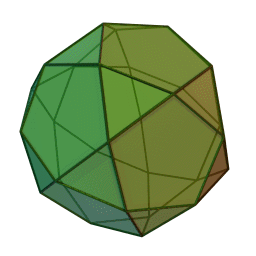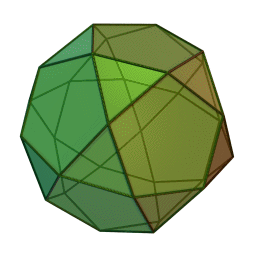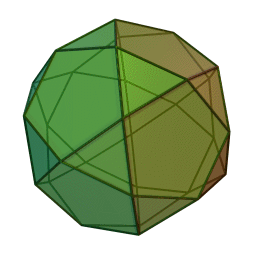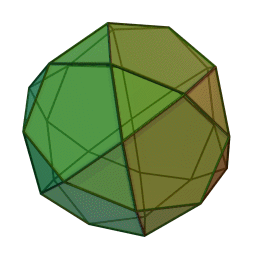
3D Conclusion
Wow, that was a lot of shapes! There were 14 to be exact. I had a lot more fun writing this than I expected and I actually learned something new while doing my research and fact checking, that being the compounds besides the stella octangula. I hope you enjoyed it.
Four Dimensional Polytopes
"Polychoron" is the name for a 4D polytope. The simplest six are as follows, they are the 4D platonic solids. With the new dimension, faces are no longer the highest dimensional components, cells are. A cell is simply a 3D component of a polytope, just as a face is a 2D one. Side always means the highest dimensional component, so the sides of a polychoron are cells. Alright, let's go through this just like we did with 3D. Let's start at the tetrahedron: how can we fold this up into 4D? Also, before we did shapes around a vertex, but in 4D we do shapes around an edge. It's a little tricky to explain why, but it helps to think about how if you extrude 3 squares that are joined by one vertex up into 3D, the vertex they were joined around is now an edge, and you can fold the cubes up into 4D to start a tesseract.
Back to the tetrahedron. We can fold this up into 3 different regular polychora, the first being the 5-cell. The 5-cell, or pentachoron, is the 4-simplex meaning it's the 4D variant of the tetrahedron. It joins 3 tetrahedra to an edge, and has a shclafli symbol of {3, 3, 3}. It is self dual. If you need a refresher, revisit the part about schlafli symbols. This shape is a tetrahedral pyramid.

You could also fold tetrahedra into an orthoplex, called the 16-cell or hexadecachoron. This is a tetrahedral anti-prism. The shape's schlafli symbol is {3, 3, 4}, and is dual to the tesseract. It has an octahedral vertex figure and connects 4 tetrahedra to an edge. This is interesting, as it's the only orthoplex that can tile space. Sure, the 1 and 2 orthoplex can as well, but that's just because all 1D shapes can tile, and the 2-orthoplex is also the 2-cube.

Finally, you could also fold the tetrahedra 5 to an edge giving you something icosahedron like. (The icosahedron is 5 triangles to a vertex, which explains the similarity) This shape is called the 600-cell or hexacosichoron, and by side count is the largest regular polychoron by far. It is dual to the 120-cell, has an icosahedron for a vertex figure, and its schlafli symbol is {3, 3, 5}.

Next is the cube. As expected, it folds 3 to an edge to a tesseract, or octachoron. The symbol is {4, 3, 3} and is dual to the hexadecachoron. This shape is also a cubic prism.

Next shape is the octahedron, and surprisingly it does fold into a regular polychoron! The dihedral angle of the octahedron is 109.471°, which is less than 120° so it can fold into a shape. This makes the 24-cell/icositetrachoron, like the pentachoron, octachoron, and hexadecachoron, it's an n-dimensional shape which I will discuss later. But what makes this shape so interesting is that it's an n-dimensional sequence that's only regular where n=4, isn't that neat?! (technically, it's also regular when n < 3 but who cares.) The schlafli symbol is {3, 4, 3}, making it self dual. This shape also tiles space, but every version of it does in every dimension due to it's relations to the n-cube. Its vertex figure is the cube, which is kind of cool.

The dodecahedron folds into a new shape called the 120-cell, or dodecacontachoron. It folds 3 to an edge and has a symbol of {5, 3, 3}, making it dual to the hexacosichoron. It can be seen as an analog to the dodecahedron.

Now that we've gone through the six normal regular polytopes, what can we stellate/compound? Well there are 10 stellations, 9 of the 120-cell and 1 of the 600-cell. The 600-cell's one stellation is called the "Grand 600-cell". It has 600 tetrahedral cells, and a great icosahedron vertex figure. Its schlafli symbol is {3, 3, 5/2}. It's made by scaling up the cells of a 600-cell. The slices look so cool. Thanks to the miraheze polytope wiki for the slice gifs and projected wireframe.




Wait, but how does stellation work in 4D?
Well remember last time, where there was greatening and stellation? Now there's a third one. I like this chart but the terminology of it is kind of dumb. Greatening is still scaling up the faces, and stellation is still scaling up the edges, so scaling up the cells needs a new term. Which doesn't make much sense, greatening should be scaling up the cells. I do agree with stellation being scaling up the edges though. Anyway, when you scale up the cells that's called "aggrandizing". Faces in 4D are interesting. When I say "face" I mean a 2 dimensional component of a polytope. For example, the 24 cell has 24 octahedral cells, but octahedrons have triangular faces, so the 24-cell has triangular faces as well. These are kind of like hyper edges. The n-2 dimensional component of a polytope is also called a "ridge", by the way. So greatening, or scaling up the faces, is a kind of weird operation for a 4D shape. Somewhere between stellation and aggrandizing. Anyway here's the chart I found online, it's really amazing and the only reason this section can exist at all. Huge shout out to whoever made it.
Info about this chart: If you look at the top there's "pD" and "pT". These are the 120-cell and 600-cell, in that order. This is imporant to know. The rest of this section is just me going through this chart and explaining different bits and showing pictures I found online.
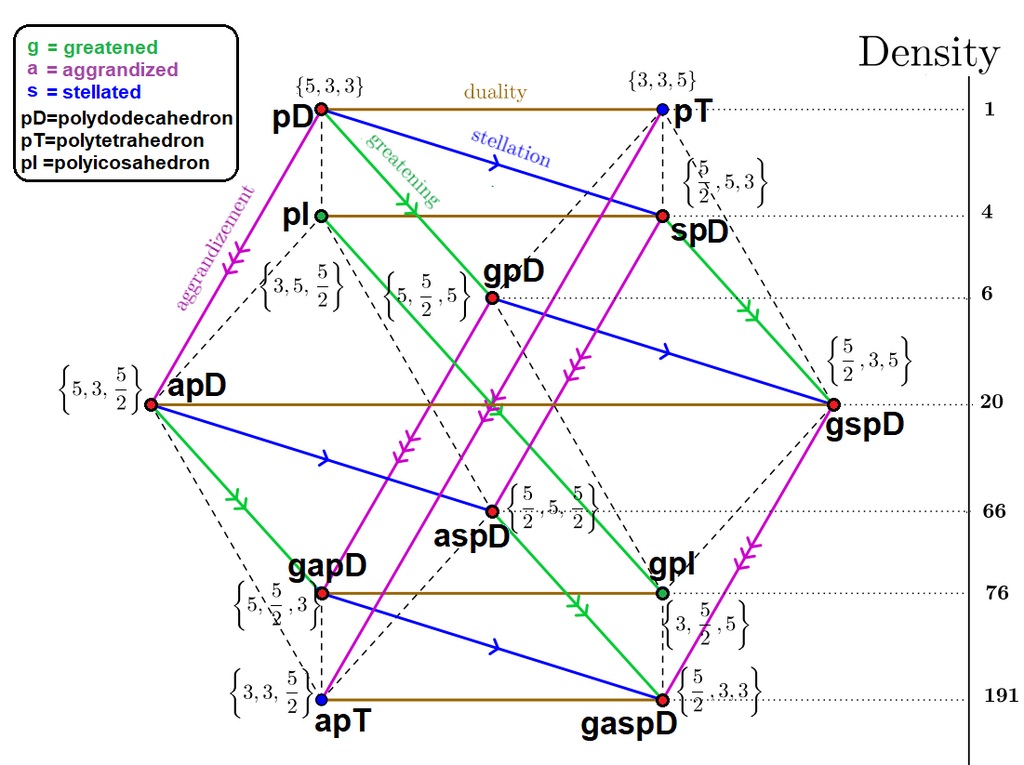
Let's cover the remaining 9 in detail! Starting with the 120-cell, if we stellate it we get the "Small Stellated 120-Cell". Its schlafli symbol is { 5/2, 5, 3 } meaning it has Small Stellated Dodecahedra for sides and a dodecahedral vertex figure. This shape can also be thought of as a pretty direct 4D analogue to the Small Stellated Dodecahedron, but it's not a great idea to try and find analogues as there are 9 stellated 120 cells and 3 stellated dodecahedra.


Next polytope, if we take the 120-cell and greaten it, we get the Great 120-Cell, with the symbol of { 5, 5/2, 5 }. It has Great Dodecahedra sides and a Small Stellated Dodecahedron vertex figure.



After that we have the last 120-cell direct star polytope, where we aggrandize it. This means scaling up its cells. Because the cells are scaled, it still has dodecahedral sides. The Grand 120-Cell has the symbol { 5, 3, 5/2 } and the vertex figure of a great icosahedron.

The next four are stellations/aggrandizations/greatenings of our already changed polytopes.
Stellating the Great 120-Cell, we get the Great Stellated 120 Cell (man gotta love standardized nomenclature). The schlafli symbol is { 5/2, 3, 5 }, meaning it has Great Stellated Dodecahedra for sides and an icosahedral vertex figure. This is my favorite stellated polychoron, it looks so smooth and blobby in slices, yet so spikey when projected. Cool shape! It's cool how it doesn't matter the order of stellation. This shape is a greatened small stellated 120-cell, but it's also a stellated great 120-cell.




Let's aggrandize the Small Stellated 120-Cell. We get a shape called the Grand Stellated 120-Cell. Its vertex figure is { 5/2, 5, 5/2 }. Which means it has Small Stellated Dodecahedra for sides, and a Great Dodecahedron vertex figure. Funny story, while writing this page I noticed that the poltyope wiki was using the wrong image on this page, and I even spoke about it on the discord server. Eventually I realized that this shape and the shape it shared an image with have identical edges, and that's why they used the same image. When two polytope share edges, it's called being in the same regiment. Huh, this shape and the Great Stellated 120-cell look really similar.

Alright you know the formula by now, so let's look at the greatened aggrandized 120-cell, the Great Grand 120-Cell! Its schlafli symbol is { 5, 5/2, 3 } meaning it has Great Dodecahedron sides and a great stellated dodecahedron vertex figure. Fun fact: it's in the same regiment as the small stellated 120-cell, meaning they have the same vertices and edges.


This is the final of these four. What if we take all these operations and put them together? Then we get a beast, the Great Grand Stellated 120-Cell. This is the dual of the Grand 600-Cell, and has great stellated dodecahedron sides, and a tetrahedral vertex figure. It is the only stellated polychoron with a 120-cell for a convex hull, which is kind of cool. The symbol is { 5/2, 3, 3 }. This shape is kind of a 4D version of the Great Stellated Dodecahedron.



Alright just 2 more! The first can only be created as the dual of the Small Stellated 120-Cell. This shape has a symbol of { 3, 5, 5/2 }, meaning it has icosahedron sides and a Great Dodecahedron vertex figure. That's how it got the name "Icosahedral 120-Cell". I'm not showing the wireframe projection model here since it's just a 600-cell, which would be misleading. Actually, most of these stellates shapes that are missing wireframe models are not shown because they're in a regiment with the 600-cell.



The second of these shapes is created as the dual of the Great Grand 120-Cell, or by greatening the Icosahedral 120-Cell. Because of this it is called the Great Icosahedral 120-Cell. The symbol is { 3, 5/2, 5 }, meaning it has Great Icosahedron cells and a Small Stellated Dodecahedron vertex figure.




Wow! That's all 10 regular stellated polychora! Now for the compounds of 4D. There are 7.
4D Compounds!
The first one is two pentachora. A pentachoron is self dual, so by having the pentachoron and its dual on top of each other, you make a regular compound. This is the equivelant of the hexagram or stella octangula.