The N-Op Polytope Naming Scheme
Why
The standard polytope naming scheme sucks. As far as I can tell, there are a set of suffixes for the rank of a polytope, and a system to go from an integer to a prefix. These are then attached to get the platonic solid names, using the facet count for the integer. For archimedeans they do [operation polytope] sometimes, but more often they just do some crazy inconsistent thingy, like "cuboctahedron". This is sometimes better but agh the inconsistency!
For example, the triangular antitegmatic icosachoron. This means "the 20 sided polychoron with triangular antitegum sides". That's a very long name for such a simple shape! Also, it having 20 sides isn't that important. I mean it's one of the first things I want to know about a polytope, but so is vertex count. That leads me nicely into the first thing I want to talk about, which is "what do we care about in a naming scheme?", but I want to shit on some more examples first.
The rhombicuboctahedron is a convex uniform polyhedron, and yet it is given a heptasyllabic name. This name tells you it has something to do with rhombuses, cubes, and octahedra. This name is actively bad as it has nothing to do with rhombuses. I have learned that the reason it has "rhombi" in its name is because it has square faces that correspond to the faces of a rhombic dodecahedron[0], and that's just plain silly! I knew what a rhombic dodecahedron was and couldn't reason that out myself.
What Do We Want?
Well, our primary goal should be making most shape names short and easy to pronounce. Our second most important goal is making our names comprehensible. Our third most important goal is making them easy to generate and expand on your own. But those goals are vague and broad.
Refining them further, what I really want is for the symmetry group and rank to be the most obvious things, followed by the actual shape details. I'm keeping the scope small, this only covers archimedean and catalan solids in n-dimensional space. There will, unfortunately, have to be some memorization, as this is unavoidable. Can't have names based off the platonic solids without naming the platonic solids.
The System
Wherever there's a name of a base shape in this system, it can be swapped with anything of your liking. This is to make this system flexible and more usable. Some people won't want to say my crazy names but still like the rest of the system, and that's perfectly okay!
Okay so now I'll get into the actual system. It works on Coxeter-Dynkin diagrams, so if you don't understand these it's not very usable, but you can just memorize all the names and notice patterns, so it's like the bad system but the names are shorter. (Mostly in character count, but usually also in syllable count).
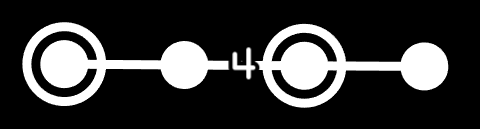
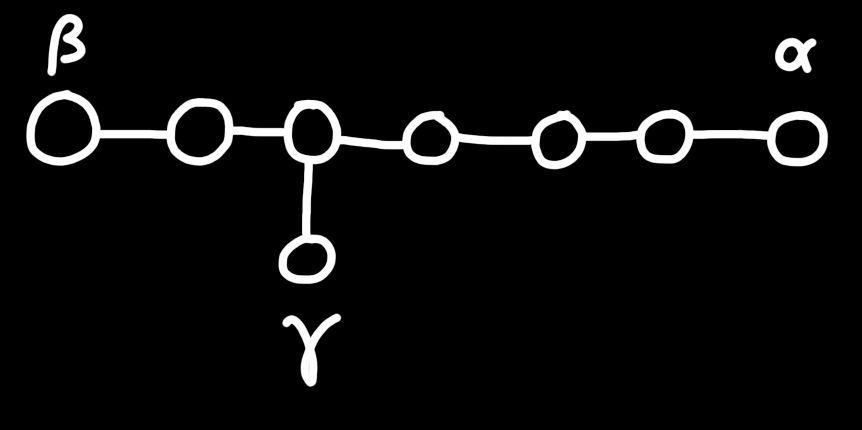
Above is the Coxeter-Dynkin diagram for the cantellated 24-cell, which the polytope wiki calls the "small rhombated icositetrachoron" (11 syllables), and normal people call it the "cantellated 24-cell" (8 syllables). My system basically names ringless CD diagrams with a specific direction and then gives a number to them based on the ringing of the nodes, based on binary numbers. This is REALLY great if you have binary memorized. (This system is really great for me and maybe you too but I understand it's niche)
So there is this one kind of confusing hiccup which is that the binary is backwards. For example, o4o3o3o is the tesseract, but I want "1" to correspond to nothing, because "1" is the identity, so x4o3o3o is called the 1 op tesseract, even though that's backwards. Of course, "1 op" is omitted because it's the identity. As mentioned before, you can also call this the 8-cell, octachoron, 4-cube, etc.
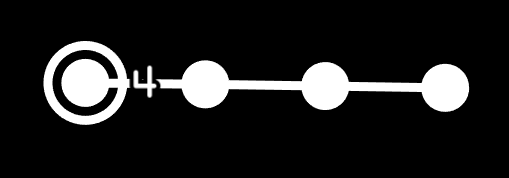
I did this because I want the 4 to be first on tesseract, and last on 16-cell, but I also want 1 op to be "self".
So, as you might guess, the CD diagram above is called the "5 op 24-cell" (6 syllables). Most of those are just from "24-cell", so you can take things further and use OBSAs, and call it the "5 op ico" (4 syllables) for max efficiency!
But, we could also call it the 2 + 8 or 10 op ico, by reading from the other direction! How do you decide which? Well, the smaller number is preferred, but they're both valid! This is not a problem and in fact, I think it's one of the greatest strengths of the op naming scheme! It's flexible, however you think about a polytope first is what you can say, and then it's equally easy to convert to a CD diagram in your head. Adding to that idea, an 8 op tesseract is a 1 op 16-cell, and an 8 op 16-cell is a tesseract.
Also, this system works best when you use a binary, tessimal (base 16), or other power of two base numbering system. But most of the time you will be using a power of 3.1622 numbering system, so you can write plusses when things get big. Eg, instead of "83 op" you could say "64+19 op", or even "64+16+3".
You might be wondering what "op" means. It's just shorthand for "operation" or "operator", and is pronounced like a truncation of those words.
Okay I think we're done with the basics! Now I'll show some names for you to memorize. (These are the ones that don't just steal the common terms)
Hardcoded Terminology & Snub Nodes
There are 4 non wythoffian Archimedean solids in all dimensions currently known. 3 of them are snub, and one will just have a name that you have to just memorize. I know, I know, it sucks, but it's just one more thing, and it's short, and has some meaning.
In 3D, these are just the snub cube and snub dodecahedron, which have snub nodes in their Coxeter-Dynkin diagrams. I thought these nodes were silly but they actually make some amount of sense. Basically, you only do even numbers of reflections to generate the shape, and then you distort it to make the edge lengths identical and the faces regular. Not as clean as unringed and ringed nodes, but, it's a useful concept so in my system, if a diagram has snub nodes, you say "snub" instead of op. So the snub cube is the 7 snub cube, and the snub dodecahedron is the 7 snub dodecahedron, but all snub polytopes are an alternation of the omnitruncation of some shape, so 2^n - 1 snub can be implied, and therefore omitted. In other words, my system calls these the snub cube and snub dodecahedron. (Or snub octahedron and snub icosahedron).
In 4D, we have the snub 24-cell and the grand antiprism. I really dislike "grand antiprism". I think it actively makes things harder to understand. For the sake of brevity, let's use OBSAs. The snub 24-cell has an alternate OBSA that I like a lot, "idex". The i means ico, the d means diminished, and "ex" means 600-cell. This is in reference to the fact that the snub 24-cell is the convex hull of the vertices of the 600-cell with an inscribed ico's vertices removed.
"Idex" sounds really cool, but since I have recently learned more about snubs, that has made me want to update this naming scheme to include them. See, the stuff I said about snub 24-cell is true, but it's also the alternation of the 3 op 24-cell, so it will be called the "3 snub 24-cell" from now on.
I will explain! 3 op octahedra are 7 op tetrahedra, and if you alternate those you get icosahedra, so that gives us 24 icosahedra, one for each 3 op octahedral cell of the 3 op 24-cell. Then the 24 vertex cubes alternate to give us 24 tetrahedra. There's 4 tetrahedra attached to each cube tet, and they don't get close enough to overlap, so it's just 24*4=96 more tetrahedra. And the 3 snub 24-cell really does have 24 icosahedra, and 24+96 tetrahedra!
So yeah, snub nodes are actually cool and followable, if a little unrigorous, and they break the idea that every Coxeter-Dynkin has a corresponding uniform polytope. But still! They're pretty nice, so, yeah, it's no longer called "idex" by my system.

Update 3: I have learned yet MORE about snubs! The 3 snub 24-cell is actually the alternation of an omnitruncate. It's the 15 snub 4-demicube! (Aka the snub 4-demicube, since all snub nodes is just called snub, as mentioned earlier). There's a reason you might not want to say this though, and it's that the 4-demicube has one sixth the symmetry of the 24-cell, so it's a bit like saying 7 op tetrahedron instead of 3 op octahedron. Depending on context that can be more or less correct, but since the context of this is just talking about a polytope as itself, not as an element, it always makes the most sense to view it as its most symmetrical version, with the fewest flag orbits.
What about the one convex non snub non wythoffian, the grand antiprism? Well it is also a diminishing of ex, via two perpendicular rings of 10 vertices, so instead of calling it "gap", we can call it something -dex. A polytope with 2 rings of 10 vertices is dedit, or the decagonal duotegum. It's literally the convex hull of two perpendicular regular decagons, so it's perfect to fit into ex! Anyway, "dedit" + "dex" is "deditdex"! I like the sound of this so that's what I'm calling it now. Again, this doesn't matter that much because you can call them whatever you want, but this is the Official™ tessimal op scheme term for the grand antiprism.
Fun fact from the future: Jonathan Bowers himself said my name "deditdex" is valid! Whether or not he likes the name is unknown, but, this is enough for me.

The n-dimensionals are called the n-simplex, n-cube, and n-orthoplex. The n-demicube is called n-demi, and is what we're gonna talk about next. It's suggested to use these instead of the more namey names when n ≥ 5. Eg 4-simplex is pentachoron/5-cell, and the hexateron is called the 5-simplex.
Not sure how to segue into writing this info but:
3 snub ico: 4 syllables
snub 4-demi: 4 syllables
Truly all that matters is the symmetry, unless you say 3 snub 24-cell (like I do), which is 6 syllables. I think "3 snub 24-cell" is the better name, but I wanted to update this page with the information about the snub 4-demi anyway. (And make omnisnub the default, to get rid of the "7".)
Dn and En
These stumped me for a while. How do I represent a branch???? Well I eventually went back to an idea I had at the very beginning of me trying to solve the problem. Just read one straight line, and then if the branch is ringed throw in an extra syllable.
It also took me a while because I thought I should understand the standard system first, but as I kept researching I realized that the standard system is held back by wanting to just be operations applied to simpler polytopes. My system doesn't do that and instead embraces the systematic nature of the diagrams. The standard scheme becomes a confusing mess in higher dimensions, especially with En polytopes. I honestly still don't understand it, but I haven't given it a properly thorough thought. To be fair, the names get really long and it's straight up wrong sometimes. See trim.
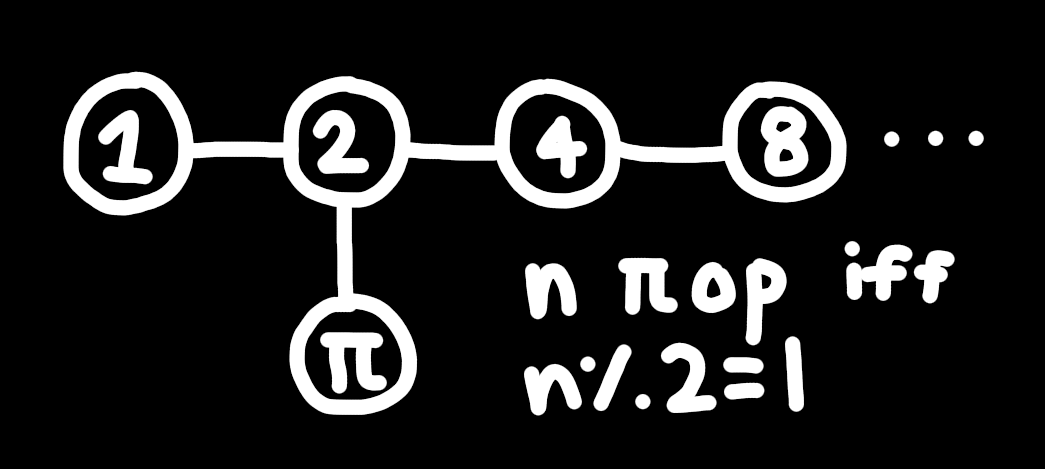
Anyway how did I solve it? Well let's start with Dn as it's simpler. You start from the side with the branch and read across to the other side with the number, and then the name of the base polytope is "r-demi", where r is the rank of the polytope. For the branch, since the first bit and the branch are swappable, you can do either but it's preferred to prioritize filling the first bit before you fill the branch. If the branch is ringed, you say π-op, or pi op, or pi-op, or piop. Adds just one extra syllable. π is just an arbitrary random greek letter. Sorry. Perhaps that's a bit hypocritical. I think I'm allowed to have my system be taught, it's excusable if the system is actually self consistent and quick etc.
quasitruncatedhexahedron pointed out to me on my discord server that π-op Dn polytopes aren't necessary, since if you ring the first node and the π node, the symmetry doubles and you get a Bn polytope. I didn't realize this because I thought there were some edge cases, but in hindsight that was quite silly. I'm leaving it in though, for semi-uniforms/archival reasons. But yeah, π-op n-demis will probably never be spoken about.
What about En? Well, I named the symmetries hexelte, septelte/heptelte (I prefer septelte because hex and hept are a bit too similar, especially if you're abbreviating things), and octelte. I'm actually really happy with these names, they're not completely arbitrary, sound nice, and are short. "Elte" is added as a suffix because these are known as the Gosset-Elte polytopes, for those not in the know.
The polytopes with just the longest side node ringed (jak, naq, fy) are the default*, so they get no suffix or the alpha (α) suffix. The polytopes with just the length 2 side node ringed (jak, laq, bay) get the beta (β) suffix. These have the bit string reversal properties you expect, the 32 op septelte-β is the septelte-α and all that. Lastly, the E symmetry polytopes with just the length 1 side node ringed (mo, lin, bif) are suffixed with, as you might expect, a gamma (γ). The elte-γ can be called the 0 π-op elte-α, and the 0 π-op elte-β. Don't worry about the greek letters, you can just type out "alpha", "beta", and "gamma".
*Jak, naq, and fy are the defaults because they have the fewest flag orbits. Refer to my chart for more about n-elte polytopes.
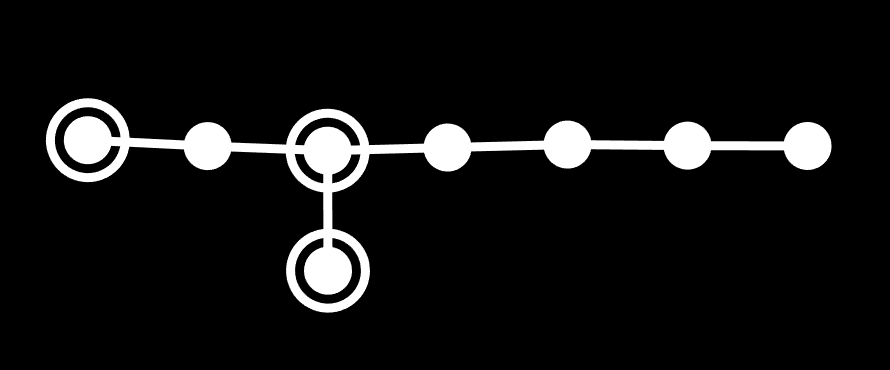
Now get ready for something really confusing: numbering from α and β are really easy, but what about numbering from γ? If you want to truncate an octelte-γ, you have to call it a 4 π-op octelte-α. Yuck. Well, here's how you do it: if the only nodes ringed are either the γ, the node connecting to that, or the two nodes connecting to that, and the ring state of those last two are the same, you can name it from the γ.
That was a little dense so I'll give some examples. The Coxeter-Dynkin diagram below could not be named from the γ node, only the α or β nodes, because it contains ringed nodes that are not 2 away from γ. That rule doesn't generalize to the α and β nodes though, so it's more correct to say we can't do it because it contains ringed nodes that are more than 1 away from the branch after γ.
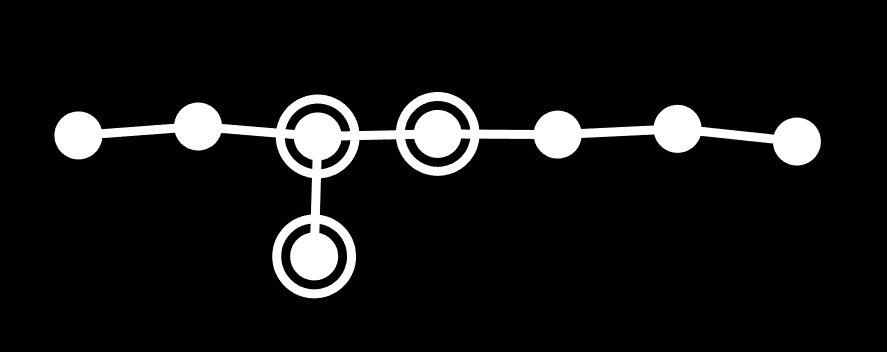
Then the last rule is that the two 4 op nodes from γ must be the same, since you can't add 4 and also not add 4. For example, the diagram below cannot be named from γ. It must be called the 12 π-op octelte-α.
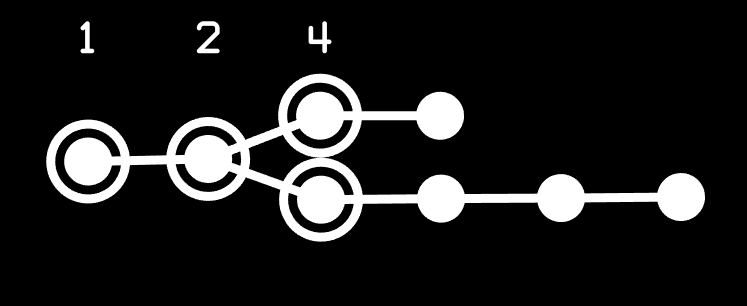
Oh wait, I guess I didn't explain how the numbers work. So, once you've determined that the Coxeter-Dynkin diagram is actually writable from the γ node, then stretch it out like this, and it becomes a simple binary number.
With the En polytopes explained, here are some examples.

The priority order is quite simple. First, ascertain if the diagram is writable from γ. If it is, write it from γ. If it's not, calculate if the number is larger when written from α or from β. Write it from the smaller one. If they're the same, write it from α, and exclude writing α after. I also suggest not writing the α suffix for E6 polytopes, since α = β for E6.
Catalans
Attach "dual" to the start of a shape name to get the dual of it. I really hate doing catalans dirty like this, but I really don't know what else to do with them. The deltoidal icositetrahedron, my favorite 3D catalan, would be called the dual 5 op cube, or dual 5 op octahedron.
On January 16th, 2026, I decided to change the "anti" prefix to "dual". This makes the system easier to understand, and a half syllable shorter. Keep in mind that there are lots of instances of the word "anti" meaning dual on this site, especially before then or in filenames.

The dual deditdex is really cool as well, it has strange dodecahedral wedge facets, and makes a good D100. I don't like the number 100, but I do think it's interesting that it's such a human side count. It's because 120 - (10 * 2) = 100. I think I like it because of its duoprismatic vibe and non wythoffian nature.

Conclusion
I don't know if anyone else will like this system or not. I have found it useful and like it a lot, and have had a lot of fun designing it. While I do think it's better than the standard naming scheme, it is very low scope, and I think I only like it so much because of the weird way my brain works, and the skills I have acquired. (Binary memorization and Coxeter-Dynkin diagrams).
Anyway, uh, yeah, I like it, I doubt anyone else will, and I understand it has flaws. People have been strangely aggressive and rude to me for disliking the standard names before, to the point where I had to leave the polytope discord, so I hope no one gets upset over this naming scheme. If even one person finds this system helpful or even just interesting/entertaining I'd be super happy!!
I will use this system in every future webpage. Thanks for reading.
Sources
0. Wikipedia article for rhombic dodecahedron
Polytope Wiki (a lot)