How I Thought I Solved Planar Time
While trying to solve planar time, I invented a universe I really like. I don't think it's really planar time anymore, it's just E3xS with some weird extra laws on top, but I may still refer to it like time occasionally, as while it is a spatial dimension, it feels kind of time like in vibes. This webpage is an attempt to explain how I found it, and how it works.
What's Planar Time?
So you know how we use time lines to visualize time because it's linear? You only need one value to describe a point in time, and the present is a point, moving forward at 1 s/s. We're gonna ignore relativity because it complicates things. What if there were two dimensions of time? Well before defining this rigorously, let's just think about it from a logical perspective. With 2 dimensions of time, I suppose the present would still be a point, and since each time axis has a past and a present, and there's two time axes, that would mean there's 4 regions of time.
In the past-past quadrant, we have events that could have caused or influenced the present. In the future-future quadrant, we have events that could have been caused or influenced by the present. In the two mixed regions, we have events that affect the future, and are caused by the past, but also aren't the present. Or something, I'm not sure. This is very strange to think about.
Okay so how does this work in actuality? Well I imagine it like this, every particle duplicates itself an infinite number of times and each new particle moves a step forward in every angle of time in the 90 degree arc between t1+ and t2+, then physics happens as normal, except there's an infinite continuum of velocities instead of just one.
Here's the rub: What happens at (1, 1)? Well, the particle takes every path possible to get there, but interacting with other particles in that time must change its path, but every point can only have one value. Everything falls apart because of the one core problem: these paths are still linear, and they must merge. I have yet to find a way to merge them, or a version of physics that never needs merging and everything just agrees. And not for lack of trying! Me and my friends have thought about this on and off for over 6 months now.
If you do anything narrative based with it it kind of works, but it feels like solving a puzzle, as you have to be careful not to contradict yourself. My friend Kronos Dolphin/Kronosta made this 4x4 planar time story, starting from the bottom left, any combination of up and right moves creates an almost sensible story. I'd make my own, and I have before, but this is way funnier than anything I could hope to make. I'm thankful he let me use this lol.
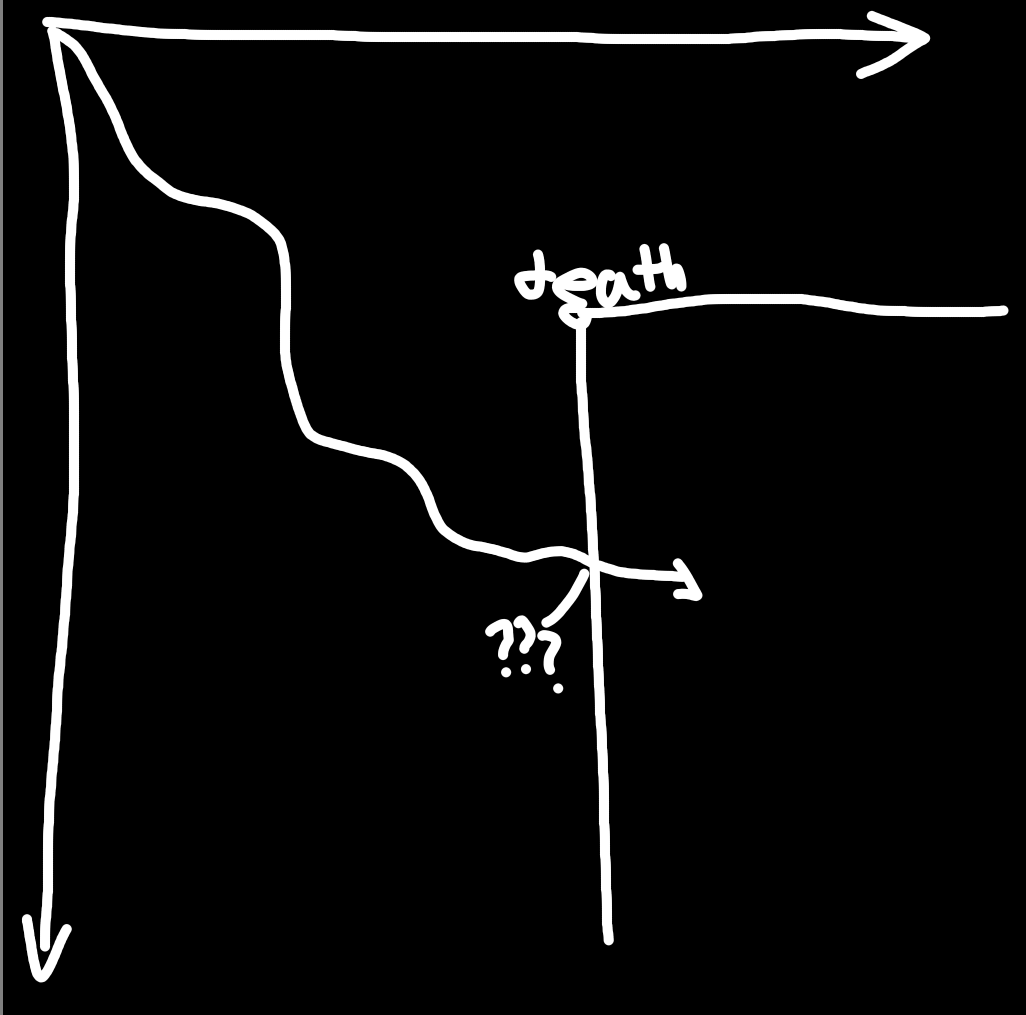
Also, death. How does it work in 2D time? If you die at (4, 3), the point (5, 6) is reachable without reaching the death point, but is after your death. What happens when you cross that boundary?
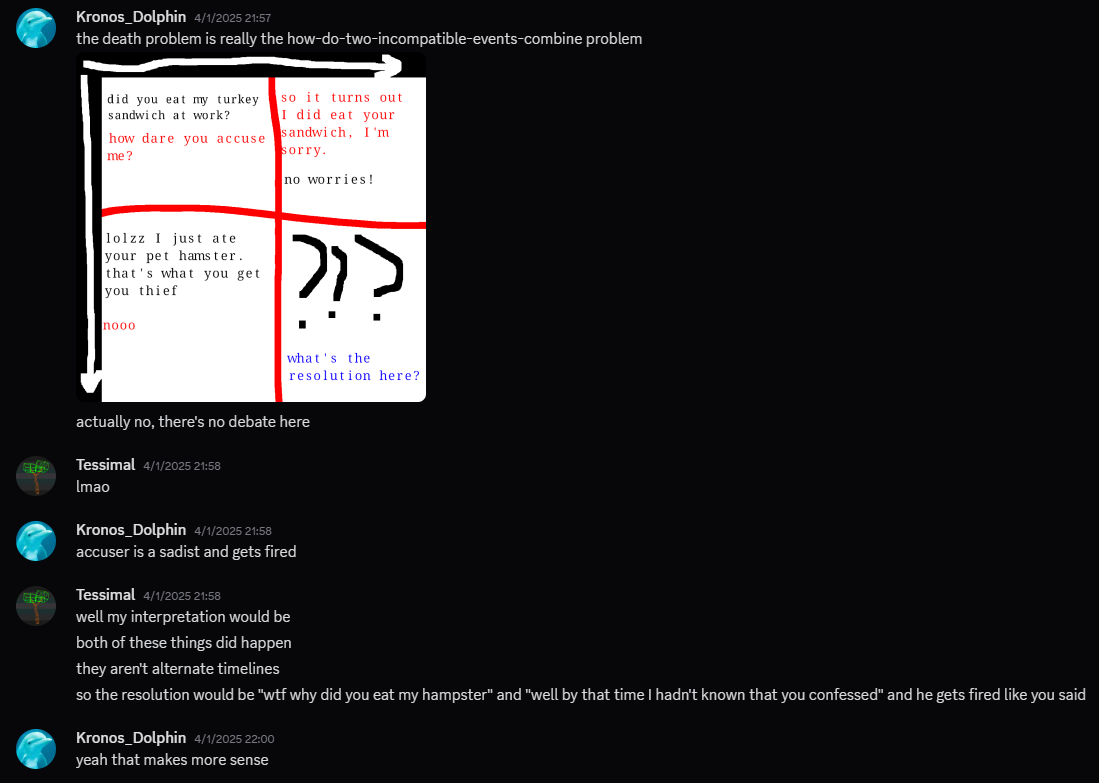
Sometimes, the merging issue isn't really a problem, as shown in this conversation. (I got permission to show this, if you're the type to care about that stuff)
With all of this, I think it's clear to see that this implementation of 2D time, while intriguing and the most natural, isn't logically consistent. I've tried to fix the merging problem with a square grid of discrete time coordinates, where time processes once cell down and one cell to the right, and then interpolates for diagonals, but that introduced a lot of friction to everything. Honestly, it's the same problem as the death thing. What happens when you cross the boundary of something's future shadow? Anything you do will have an abrupt sudden change, or have so much friction that no force can do anything in the universe.
If you still like this version of 2D time, what I'm calling "balanced" 2D time, you should check out the conlang Saj. Unorthdox Kitten also featured balanced 2D time, in this video at this timestamp. By the way, I figured this version of 2D time out before seeing either video, and I assume The Zip Creator didn't learn from Unorthodox Kitten. Not trying to be petty like "erm I had the idea later but I didn't KNOW about the videos so I'm still cool", just mentioning this because I think it's interesting that 3 people came up with pretty much the exact same system from the same idea, despite it not actually being logically consistent. Usually when it's not logically consistent, there's no clear extrapolation.
Before the next chapter, I want to mention another popular 2D time model. It was popularized by Greg Egan, and is used in his book Dichronauts. I'm only going to touch on this briefly, since I actually know nothing about it, so take everything I say with a grain of salt and just read his article if you're curious. Anyway, you know how in order for two objects to affect each other, this must evaluate to true? x2 + y2 + z2 + -(t2) < 0? Where x, y, and z are the distance along those cartesian axes, and t is the distance in time? No? Well it's just the formula for the future and past light cone, so while I didn't recognize the formula either, I know what that is and you probably do too. Also, this is assuming that the units make c = 1.
Well Dichronauts comes from asking the question "okay but like what if one of the spatial axes was negative too?" And some weird shit happens! I recommend just checking out his page if you're interested, and I've heard his book has great world building. Come to think of it, I should give both of those a proper read, the webpage is a bit too technical for me but the subject matter seems very interesting. If I made a mistake, please let me know so I can fix it. Dichronauts isn't really 2D time in a sense, as in my opinion the new dimension is far too space like. But honestly, after thinking about my own unique take on 2D time (not balanced planar time, I will get past the preamble of this webpage soon dw) some more while writing this... my second axis of time is fairly space like too. Oh well. Anyway, now that I finally have that "uh you forgot to mention..." out of the way...
Why Didn't Balanced Planar Time Work?
After much deliberation, I've come to an answer. Now, I know what I'm about to say is scientifically wrong, but I think it might not be? Maybe? I'm not sure, relativity is confusing, and this seems to work as an explanation for why balanced planar time doesn't work.
Here goes. I think the reason it doesn't work is that time isn't one dimensional, because it's not a dimension. It's helpful to pretend the universe is a simulation for stuff like this, so I'll use those terms to make things quicker for a second. As the universe chugs along, it crunches the numbers and calculates how every particle moves and changes over time. Except it's actually updating a wave function, but that's not important right now. Each "frame" of the universe happens after the last, and so it can be arranged as a one dimensional line, but it doesn't feel like it is one literally. The past doesn't exist anymore and the future doesn't exist yet. Except relativity says that's wrong and time is more spatial than thought before. I'm really unsure about this explanation, but it seems to work for this.
After all... you can't move backwards in time, only forwards at (usually) the same rate. It just doesn't act linearly, it acts more like a point. Or rather, time is 1 dimensional, but the present is a point. Maybe, like knots only working with n-2 surfaces, time must be 1 dimensional, and the present is n-1 dimensional when time has n dimensions. What would a 1 dimensional present look like?
1 Dimensional Present?
I'm going to attempt to describe a universe where there's still one "dimension" of time, but perpendicular to that there's a 1D present rather than a 0D one.
I struggled with this for a bit, often reinventing balanced planar time or normal linear time, but in the end I came to what I've been building up to this whole webpage. A thing that... barely works!! But allows for cool shit and weird properties! The solution? The other time axis of the present should be short, circular, and not have a forward/backward. Every point on it should be equal. You know, like the present.
But as I've realized after writing this webpage (I learn a lot when I write a webpage), the circular present isn't really like time at all. I mean sure it's not claiming to be, it's the present, but all this universe is is E3xS but every particle is a circle with circumference equal to that of the S axis. It really does feel and act like a present, but it is fully, unambiguously, a spatial dimension.
If you don't know what E3xS means, it's standard non euclidean notation. E3 means 3 dimensions of euclidean (normal) space, S means one dimension of spherical space (so the 1D surface of a circle) and the x means you multiply them together. In topology, multiplication refers to cartesian products. In other words, E3xS is a four dimensional geometry where 3 axes are infinite and euclidean (normal), and one axis also acts euclidean, but it's finite and the start and end wrap. It's the inside of a cube where the top face and bottom face are the same face, and it's infinitely wide on the other two axes.
Circular Present Time
The axes are t and u, t is time, and u is the present. BEHOLD THE ALMIGHTY TIME CYLINDER!!
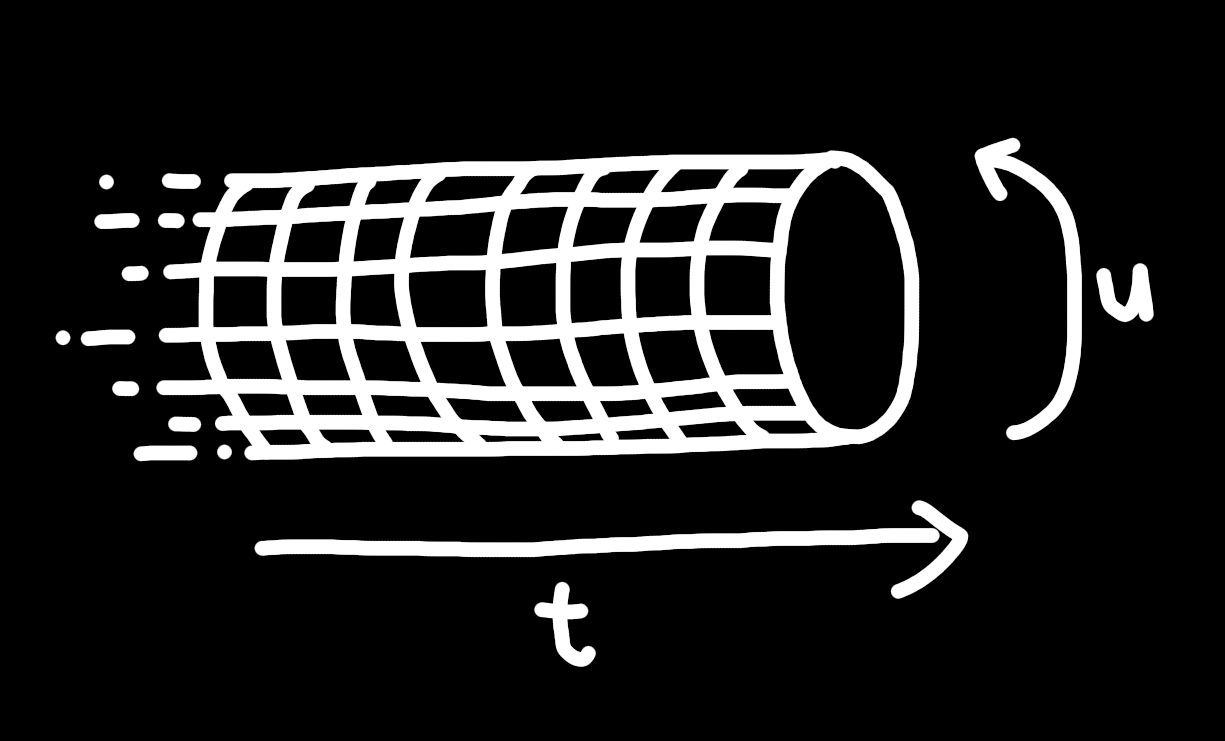
The u axis should be on a fairly human scale, 3-6 meters minimum, 18 meters maximum. These values aren't hyper specific by the way they're just base 6 round numbers. It's not that it doesn't work when the present is astronomically long, or atomically short, it's just that things get a little too weird when it's long and things get a little too normal when it's short. Like there's some problems with this idea, and they are harder to sweep under the rug when the present is long. It can even be infinite, or any manifold, like a sphere, clifford torus, or H2.
I think 6 meters is the perfect length for the u axis to have, and that's close to tau, so let's just say the time cylinder has a radius of 1 meter.
Basically how this circular present idea works is that every particle is extruded along u to wrap back around on itself, and it's stretchy. u is simply used to describe more time lines that are right next to each other, and as they get further apart they affect each other less. It accomplishes this by being a spatial axis that everything is extruded in, that wraps back on itself.
The simplest example is two particles in space. We'll set the first one at x=0 for every point u at t=0, and the second one will be the same but x=1. As there's no variation on the u axis, this is equivalent to normal time. If we set the first particle moving towards the first at 1 unit per second at every point in u, it's still identical. Every linear slice shows the particles getting closer, and every radial slice shows the two particles at the same distance.
Let's make things more interesting. They're both still one unit apart, but at t=1 we apply a force to the first particle so that it's moving at 1/s, at u=0. As this is actually a 4D spherinder rope, accelerating one point accelerates its neighbors. Values of u very close to 0 have a velocity of almost 1, and as you get further out, it quickly drops to near zero. The velocity is interpolated, and so is the position. This means that the amount of force you give in won't quite accelerate the mass to the normal speed it would otherwise, but no conservation of energy is broken, as every particle just has more mass, along u.
At t=1, u=0, the two particles collide, transferring all of the velocity of the first to the second. This change in velocity from 1 to 0 takes time to propogate through u, as u+ and u- of the particle it's still moving at a little less than 1 unit per second. They slow down a bit but are still carrying momentum, so in quick succession there's more contacts, and now a thin region of u is where the collision happens, not just a point. Eventually the change finishes propogating down the rope, and so now particle 2 is moving at 1/s at u≈0, and particle 1's x value is at around 0.5-0.75 for all points of u, with velocity zero at all points of u. Slowly, the rubberband effect will pull particle 1 to have the same x value for every point along u.
If you pull on an object at a specific point along u, it will take more force than it would seem, as everything has more mass than it appears to (because u is a spatial axis and objects have density). Note that because of a little thing called "bending stuff to get the universe to behave the way I want it to", objects are very not dense along the u axis, but this is another reason I suggest setting the u axis circumference to something small. Also muscles would be affected by this too so I imagine them to be strong enough to counteract the effect anyway. Picking it up from a single point instead of all points is harder though, especially with the friction.
This force of the tension scales with mass and distance, so it shouldn't be hard to pull the particle, it just takes marginally more force at first, as all the other points of u begin to accelerate. Once it gets up to the speed you're pulling it at, it acts just like a normal particle I'd think. Once you stop, the other parts in u are still moving forward and would go too far forward before settling.
Imagine a rock on a cliff. If someone pushes it down at all points of u, which, I say "at all points of u" a lot, let's define some terms now. Okay so a universal action is something performed in the same way at the same time at every point of u. A sharp action is an action performed at a single point of u or very narrow span of u. A wide action is an action that spans a large but not complete percentage of u.
Back to the rock. If someone universally pushes it off the cliff, it falls completely normally, save for the irregularities in the push as humans aren't perfect. If someone pushes it off the cliff sharply, well things are much more interesting. For the first second or so it falls as normal, but then the tension of u+ and u- starts to interfere, it begins to slow and more of the rock is pulled off the cliff. It behaves like a 4D circular rope. (Because it is one) Eventually, around half of the rock is off the cliff and the rock at the u of incidence hits the ground. With this the velocity of 0 is propogated some more, and the region of u where the rock is falling only expands a bit more before stopping.
So, the rock at the u of incidence is on the ground, and the rock at the opposite u is on the cliff... so what about the nearby u values? Well, they're in the air! The 4D rock rope sags down, creating slices where the rock is floating in mid air. This is really cool to me and I hope that with my explanation it feels intuitive as to why this happens. Others might say this is proof this doesn't work, but I think it's fine, and this time system I've defined isn't really planar time, but it's certainly interesting.
What if you tried to touch the floating rock? Well, pulling it would have to be a sharp action, and when you do this you'd feel the tension. If you let go it'd swing back and forth in the direction you pulled it. But if you pull hard enough, hard enough that the velocity travels all the way to the first point in u where it's still on the cliff and still has enough force to overcome friction, well it comes loose and more of the rock falls. Then you'd feel the weight of the rock pulling downward, and given the drawing, it may be too heavy to hold.
This is a picture I drew showing the rock in mid air.
The last thing I want to talk about (for now, if I come up with more scenarios I'll talk about it on my website) is how I imagine people would work. Now, as I've said earlier, the uh, science of this is a bit shaky. You could say it's held up in mid air by nothing. Anyway, you know how you have 2 eyes but it gets processed into one visual experience? And you have two ears but it gets processed into one auditory experience? And so on... I imagine this is because the present is 0 dimensional. A point has a 0-volume of 1 so you get 1 sensory experience. The 0-volume of the surface of a circle is infinity, so I imagine these people would experience every point of u at any given circle t at once. This isn't like Arrival or anything, as they experience all of the present at once, not time. And it's more of a spatial dimension anyway.
This means that looking at this cliff scene, they wouldn't think of the rock as floating. They'd see where it's held up (the cliff) and why it's sagging (the rock on the ground). You can imagine their vision as volumetric, if you choose to do this, you could say they actually see the 4D rope, and would be able to understand four dimensions. I don't think they could though, because of the extrusion. They certainly would have an easier time understanding four dimensions though.
Neural outputs work the same way. They can specify "I want to move my arm like this at this point u" or "I will say these words in this time span of u". Together these two circles of inputs and outputs make up the way they see and interact with the world, and I imagine it would do some really fun things to culture and language. The background of this webpage is a single circular moment in time, of a person playing catch with their friend. And I want to mention that this part is more of a world building element, as I haven't actually been able to come up with a good explanation for how a brain could work like this, since all the neurons should be prisms. Maybe the neurons are in different spots along u, making a strange 4D nest of wires, and maybe electrons aren't extruded like everything else, but I believe that would ruin chemistry.
What if someone ran sharply? What would happen to the rest of their body? I imagine they'd feel a tug, and just as when you get pushed, their brains would instinctually follow the leash, but imagine that they use their free will to stand their ground. As they get further from the rest of their body, the pulling force gets stronger and stronger, until they can't move further. The rest of their body is far heavier than the one part moving forward, so the rest of themself would be the anchor and so they wouldn't be able to overcome their own weight. Also, how far they go depends on how sharp the action is. As in, at what point do they let the rope go slack and stop holding themselves firm to the ground. If it's very sharp, they can't get very far. If it's very wide, they can go really far.
What if they, at this point, leaped forward? I imagine the parts of them close to the sharp leap might fall over towards them, but ultimately, the person would go forward, and once disconnected from the ground, friction stops acting in their favor and they get pulled closer towards the bulk of their body. Anyway, I drew a picture of a person trying to run from themself and I think the concept is metal as fuck. You can't run from yourself, but with my universe, you can try. This could easily become something scary if it wasn't one coherent sentience controlling all of the body.
Another really cool thing about people is death. Imagine a bullet is misaligned with you in such a way that its path only intersects you at one point in u. That part of you would certainly die, at which point... what happens? Well, as explored previously, you can't run from yourself. So you'd have to drag your corpse around. But that's not sustainable, and you'd think it would start to rot. But how would it? The bacteria need to enter your body, but u+ and u- of your corpse everything is sealed, so they wouldn't be able to get very deep into the wound. I really don't know how death would work, my intuition says the rot and death would spread as you lose an ever increasing arc of your input and output, but I'm not sure. I wonder how that would interfere with your brain function.
Also, the parts of yourself near your dead self would have their limbs interpolated towards the pose of your corpse. I imagine controlling those parts of yourself would feel like doing a fireman's carry, but the person is duct taped to your four dimensional side. Aka, you're twice as heavy.
If you break something in this universe non universally, its shards will be sort of connected, and it'll be a loose cloud you can carry around. As objects get chipped and age over time, there would be a small cloud of shrapnel around them.
Conclusion
As with most times I think I solved planar time, there's always some big flaw or it's not actually planar time. I believe planar time, the way I want it to work, is impossible logically. But what I've shown off in this webpage, while not actually being very time related, is very cool and somewhat logically consistent, definitely good enough for a story or a basic physics sim. I hope you enjoyed reading this page, I put a lot more effort into it than I usually do, with all the drawings and what not. I might make more content about this universe. Thanks for reading!