Cursed Digits & Their Uses

You are not required to use the digits 0 through b-1 in base b. That's not a rule, it's a standard. The most common example of numbering systems that do not abide by this are bijective systems. Systems where b is notated with a single digit. Bijective decimal goes 9, X, 11, 12. Twenty is 2X. 100 is 9X, or if there's a zero, X0.

Going further, those digits don't even need to be integers. they can be any real value. Though if you use different non integer numbers, I'm not sure if integers can be represented anymore. I think they can in most cases, by using numbers past the radix point, but I'm not totally confident and I'm clueless as to how you would calculate their representations. This is math I found on my own rather than through someone or something else.

0.'2497 is a Deal-Breaker

The reason why I don't like dozenal is because one fifth is 0.'2497. But, here's a stupidly simple question: what's one qaurter in dozenal? It's 0.3. But what is 3? It's one fourth of 12. So we could write it like this: 1/4 = 0.(12/4). "3" is just a symbol that represents 12/4. 9 is just a symbol that represents 12/4 * 3. X is just a symbol that represents 12/6 * 5. Anyway, my point with this is, what if we add 4 new digits to base 12? One for each multiple of 12/5.

We'll notate them with A, B, C, and D. This is deeply cursed. A number without a radix point is now not necessarily an integer. A0 in dozenal is 28.8 in decimal. A is 2.4, B is 4.8, C is 7.2, and D is 9.6. These look nice since I'm using base 2 * 5, for your convenience. But now 1/5 is 0.A! That's nice and simple. Also, to test if a number is an integer, add all of its digits and check if that is an integer. To save time, only add the funky ones.

We did it! With the power of floating point digits, we were able to sort of amend dozenal's biggest flaw. Only problem is there's no divisibility test for 5, which is arguably more important than writing one fifth nicely. Also, having these crazy digits screws lots of stuff up. Let's do some math with this dozenal variant, which I will call 16 digit dozenal from now on.

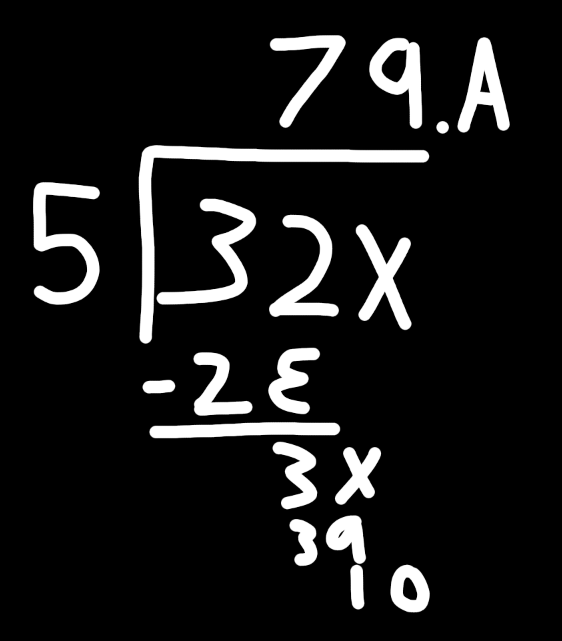
That was actually my first time doing math in dozenal. (Except for like one addition example I made for a video a few months ago). So I can't compare doing math with these digits vs without, but it did feel pretty easy seeing "10/5" and just writing A instead of having to think about it. In case this wasn't clear: I am NOT advocating for dozenal! Divisibility tests are more important, and this does nothing to rectify that. This is just a mathematical curiousity that only fixes the fractions. Also I did some decimal conversions and used a calculator afterward, my math is correct.

I tried to do some more math (a multiplication problem involving two numbers with some of these digits) and uh, it's basically impossible. 2.4 * 4.8 is hard to do in your head in decimal, imagine doing it in dozenal where one fifth is 0.'2497! A one digit multiplication problem resulting in fractional components screws everything up. Yeah, this is definitely cursed. Funny that I thought they might actually be useful for a second...

6 Digit Quaternary

Maybe these would be better in a smaller base, one that actually does the fraction in question well. Let's try adding two digits to quaternary, one for 1.'3 and another for 2.'6. Let's use Ɛ for 4/3 and λ for 8/3. The first is because its related to 3, and the second is for no reason. I just think lambda is pretty.

First most obvious thing is that 1/3 now has two valid solutions. Either 0.'1 or 0.Ɛ. And one and a third is either 1.Ɛ or Ɛ.